Author Archives: Sybil Shaver

Test 3 review materials

Test 3 is scheduled for Wednesday 15 November, the first hour or so of class.

Here is the survey for you to use to plan how to make best use of the resources available to you: this is for your private use

ThinkingStrategicallyPreTestSurvey

Here are the review self-tests, with some errors corrected: notably, problem 2 should have referred to “sequences”, not series, and that has been fixed.

MAT1575Test3Review

Here are the answers, with extensive hints and partial solutions for the first Self-Test: less detail is given for the second self-test

MAT1575Test3ReviewAnswersFall2017

 

Please let me know if you find any errors in these!

 

Here are links to some additional resources:

On Taylor Polynomials:

Video from PatrickJMT (on YouTube, so may autoplay another video after)

Taylor Polynomial Ex. 1

Taylor Polynomial Ex. 2

Paul’s Online Math Notes on special series (geometric and telescoping, mainly)

 

Wednesday 8 November class

Topics:

• Theorems about convergence/divergence of series

So far we have the following:

• The integral convergence test (from last time):

• (Direct) Comparison test: this is very similar to the direct comparison test for improper integrals where the upper bound of integration is infinite.

• Limit Comparison test: this is also very similar to the limit comparison test for improper integrals where the upper bound of integration is infinite.

Strategy to choose a method: I would usually try them in the order given above. If it is easy to do integral test, use that. (Maning, you can easily figure out whether the integral converges or diverges.) If that is not easy, see if there is a direct comparison with some series you know about (a geometric or p-series, especially). If the direct comparison does not work because the inequality goes the wrong way, it is very likely that you can use limit comparison.

I worked these examples using the integral test:

The harmonic series \sum_{n=1}^{\infty}\frac{1}{n} diverges, because we can compare to the integral \int_{1}^{\infty} \frac{1}{x}\textrm{d}x and we show (or remember) that this diverges.

Note: the harmonic series is just a p-series with p=1. Similarly, we can show that any p-series will converge if p>1 and diverge if p\le 1, by comparing to the appropriate improper integral.

 

Show that \sum_{n=0}^{\infty} ne^{-n^{2}} converges: this example will show you a couple of important considerations in using the integral convergence test which you may be tempted to skip over, so study it carefully.

Unfortunately, the LaTeX rendering in WordPress is being very glitchy so I cannot just type this example in this post. I have made it in pdf form for you:

MAT1575IntegralConvergenceTestExample

You can also find a discussion of this example in Paul’s Online Math Notes. (example 2 on that page)

Here are some links to relevant parts of Paul’s notes:

Integral test notes

Integral test practice problems

Comparison test and Limit comparison test notes

Comparison test and Limit comparison test practice problems

It’s very good to use those practice problems to test yourself, as you can see his solutions right away when you finish. Testing yourself is one of the best ways to learn.

Homework:

• Review the examples discussed in class for all 3 of these tests. You can (and should!) also look at Paul’s Online Math Notes for even more examples and practice problems.

• Do the WeBWorK assignments on Intro to Series 2 (which has been extended) and Comparison Tests. Another assignment was also posted but you do not need to work on it yet.

• Don’t forget that Test 3 is scheduled for next Wednesday. The review materials will be in a separate post.

 

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

Test 2 solutions and redo problems (bumped up to top of posts)

Here are the solutions to Test 2, according to the version you have (look at the lower left on the cover sheet)

MAT1575Test2a-solutions    version \alpha

MAT1575Test2b-solutions   version \beta

Here are some errors that were frequently made, which I did not mention in those solutions:

• The integral \int \frac{\textrm{d}x}{x} is \ln|x| + C: the absolute value signs are essential! Too many people left them out. This can cause you to think a definite integral doesn’t converge when it really does. Be careful!

• The definitions of the improper integrals where there is a singularity of the integrand (the range is unbounded) involve one-sided limits: it is important to take the correct limit, because the two one-sided limits may not agree with each other and it is possible that one of them exists and the other does not. Please look at the definition given in the textbook on p. 337 (Definition 25) or see in Paul’s Online Notes: Improper Integrals (scroll down to “Discontinuous Integrand”) where there is more detail.

• Problem #6 specifically asked that you use a comparison test to determine whether or not the integral would converge. Some people just went ahead and tried to compute the integral. This was wrong (because it was not what was asked for) and a waste of time. Please read the instructions to the problems. For comparison tests, here are Paul’s Online Notes: Comparison Tests for Improper Integrals.

• In general, there were a number of test papers where many steps were missing and I am quite sure those steps could not be done in your heads.I do not know how this came to be, but please know that in the future I will have to make sure that people are not using extra sheets of paper and do not have their cell phones visible. I am very sorry to have to do this, for the majority who are honestly doing their best and following the instructions. Please read all the instructions on the cover sheet; you are responsible for following them. In particular, if I cannot see how you got your answer or any part of it, you may receive no credit: if in doubt, write it out!

It would not be a bad idea to look at both versions of the test solutions. Only two problems were actually different, and some were moved around.

If you did not receive full credit (a total of 40 points) for problems 5 and 6 on the third page, you have the opportunity to work similar problems to increase your score. In order for your score to increase, these must be done totally correctly and showing all work (except what you can easily do in your head: if in doubt, WRITE IT DOWN!)

These problems are due by the start of class on Wednesday 8 November.

MAT1575Test2-redoProblems

 

Monday 6 November class

Topics:

• Some important types of series:

Geometric series

p-series

Telescoping series

• Another theorem about convergent series:

If a series converges, then the limit of its terms must be 0.

Therefore if the limit of the terms is not 0, the series does not converge.

Note: when using theorems about series, please be very careful to distinguish the terms of the series from the partial sums of the series!

• Intergal comparison test for convergence of a series:

Consider a series \sum_{n=1}^{\infty}a_{n} whose terms are related to a function a(x) defined and positive on the interval [1,\infty), so that a(n) = a_{n}. Then \sum_{n=1}^{\infty}a_{n} converges if and only if the improper integral \int_{1}^{\infty}a(x)\textrm{d}x converges.

Example: we can use this to see which p-series will converge: the p-series \dislpaystyle\sum_{n=1}^{\infty}\frac{1}{n^{p}} can be compared to the integral \displaystyle\int_{1}^{\infty}\frac{1}{x^{p}}\textrm{d}x, and we know from our previous work that those integrals converge when p>1 and diverge when p\le1.

 

Homework:

• Review the examples discussed in class. It is important to be able to recognize the geometric series, p-series, and telescoping series, and know who to handle them. See Section 8.2 in the textbook.

• Do the WeBWorK: it is not due until Sunday, but your should definitely try to complete Intro to series 2 by Wednesday.

• There will be a Quiz on Wednesday: the topic will be these types of series!

Also don’t forget that if you did not receive full scores on Problems 5 and/or 6 on Test 2, you have the opportunity to do a similar problem for half of the missing points. These problems must be written up completely correctly and are due at the start of class on Wednesday. See this post for more information and for the problems themselves. They are absolutely no excuses due on Wednesday, so don’t delay!

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

Wednesday 1 November class

Sorry this is delayed. I’m getting persistent “formula does not parse” messages and I cannot see why. So I’m posting as is. You can probably figure out what belongs in those places.

Topics:

• Introduction to sequences – was done last time with the sub. I added a couple of theorems and definitions which are listed below.

 

• Infinite series (introduction): partial sums, convergence, and a few examples.

Definitions I mentioned:

• A sequence is monotonic increasing if its terms never decrease: they always either increase or stay the same. A sequence is monotonic decreasing if its terms never increase: they always either decrease or stay the same.

If the terms always increase, we say the sequence is  strictly increasing.

If the terms always decrease, we say the sequence is  strictly decreasing.

• A sequence is bounded If there are two numbers M and m such that m < a_{n} < M for all n. Otherwise it is unbounded.

• A sequence is bounded from below If there is a number m such that $latex  a_{n}> m$ for all n.

• A sequence is bounded from above If there is a number M such that $latex  a_{n} < M$ for all n.

We won’t be using those last two right away: but keep them in the back of your mind. Obviously, a sequence is bounded if and only if it is bounded from below and from above.

 

The theorems about sequences that I mentioned:

• Absolute convergence: for a sequence 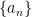\left\{a_{n}\right\}, if the sequence of absolute values 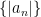\left\{\left|a_{n}\right|\right\} converges, then the original sequence 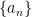\left\{a_{n}\right\} also converges.

This can be useful in determining whether or not an alternating sequence (one in which the signs of the terms alternate) converges.

• A convergent sequence is bounded: If the sequence 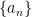\left\{a_{n}\right\} converges, then it is bounded.

(So if a sequence is unbounded, it cannot converge!)

• A bounded monotonic sequence converges: If the sequence 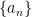\left\{a_{n}\right\} is bounded and monotonic (increasing or decreasing), then the sequence converges.

• Definition of a series (infinite series): given a sequence 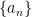\left\{a_{n}\right\}, we form the infinite sum 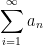\displaystyle\sum_{i=1}^{\infty}a_{n}. This infinite sum is called a series.

Note: the index does not have to start at 1. At times it is more convenient to start at 0 or some other number.

• Partial sums: The n-th partial sum is S_{n} = \displaystyle\sum_{i=1}^{\infty}a_{n}

Again, the index may not start at 1. We start it wherever the sequence naturally starts.

• Convergence for a series: A series 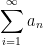\displaystyle\sum_{i=1}^{\infty}a_{n} converges if the sequence of partial sums 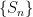\left\{S_{n}\right\} converges: otherwise, it diverges.

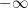Remember that when we say a limit is \infty or -\infty, it is just a way of saying that the limit does not exist in a particular way. In these cases we will say that the sequences diverges to infinity or diverges to negative infinity.

Examples I used in class:

We started out with the example on the top of p. 411. This is a very important example and will show you a lot about series, especially if you don’t already know (or have forgotten) that there is a formula for the sum. It is well worth examining in detail.

Examples:

• For the sequence a_{n} = n^{2}, n=1, 2 3, …, does the series converge or diverge?

We look at the first few terms of this sequence:

1, 4, 9, 16, 25, …

So the first few partial sums are

S_{1} = 1

 

S_{2} = 1+4 = 5

 

S_{3} = 1+4+9 = 14

 

 

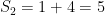
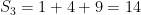
And so on. It’s pretty obvious that this is an unbounded sequence, so it diverges. Therefore the series 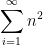\displaystyle\sum_{i=1}^{\infty}n^{2} diverges.

Note: there is a formula you can write down for the partial sums: it is the formula for the sum of the first n squares. It is a useful thing to know (or at least, to know it exists!) Here is a nice discussion of several similar formulas, including adding the first 100 whole numbers, which supposedly Karl Gauss did as a youngster.

 

• For the sequence For the sequence 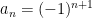a_{n} = (-1)^{n+1}, n=1, 2 3, …, does the series converge or diverge?

This is an alternating series: the first few terms are 1, -1, 1, -1, 1, -1, …

The first few partial sums are

S_{1} = 1

 

S_{2} = 1+(-1) = 0

 

S_{3} = 1+(-1)+1 = 1

 

 

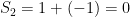
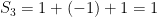
And so forth. The partial sums are clearly not converging to anything. This series \displaystyle\sum_{i=1}^{\infty}(-1)^{n+1} diverges.

Note: in the previous example, the series diverges to infinity. Here, the series just plain diverges.

 

• Consider the sequence 9, 3, 1, \frac{1}{3}, \frac{1}{9}, \frac{1}{27},…

We can find a formula for the n-th term: observe that this sequence starts with 9 and then to get to the next term we multiply by \frac{1}{3} each time. (This is an example of a geometric sequence, as is the first example from the textbook: but please don’t go looking up formulas yet! Think it through!)

So the first few terms have these forms:

a_{1} = 9

 

a_{2} = 9\left(\frac{1}{3}\right)

 

a_{3} = 9\left(\frac{1}{3}\right)^{2}

 

a_{4} = 9\left(\frac{1}{3}\right)^{3}

 

a_{5} = 9\left(\frac{1}{3}\right)^{4}

 

a_{6} = 9\left(\frac{1}{3}\right)^{5}

 

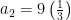
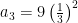
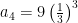
And so on, so we see that

a_{n} = 9\left(\frac{1}{3}\right)^{n-1}

 

We computed the first few partial sums in class, enough to see that although they were growing, the growth was slowing down. Since the partial sums form a monotonic (increasing) sequence, if you can show they are bounded then you have proved that they converge. This is a little harder, but it’s possible to get a formula for the n-th partial sum in a similar way to the way we got it for the first example (the one from the textbook p. 411). I leave this to you as a challenge. The trick here is that when you form the partial sums, you should factor out the 9 and write the fraction factor as a mixed number as follows:

S_{1} = 9

 

S_{2} = 9 + 9\left(\frac{1}{3}\right) = 9\left(1+\frac{1}{3}\right) = 9\left(1\frac{1}{3}\right)

 

S_{3} =9\left(1\frac{1}{3}\right) + 9\left(\frac{1}{3}\right)^{2} = 9\left(1\frac{1}{3}+\frac{1}{9}\right) = 9\left(1\frac{4}{9}\right)

 

S_{4} =9\left(1\frac{4}{9}\right) + 9\left(\frac{1}{3}\right)^{3} = 9\left(1\frac{4}{9}+\frac{1}{27}\right) = 9\left(1\frac{13}{27}\right)

 

S_{5} =9\left(1\frac{13}{27}\right) + 9\left(\frac{1}{3}\right)^{4} = 9\left(1\frac{13}{27}+\frac{1}{81}\right) = 9\left(1\frac{40}{81}\right)

 

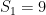
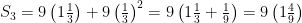
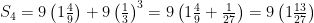
If you look closely at how we get each new numerator, the numerators are the sums of powers of 3:

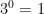3^{0} = 1 and the first numerator is 1

3^{1} = 3 and the second numerator is 1+3 =4

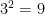3^{2} = 9 and the third numerator is 1+3+9 =13

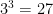3^{3} = 27 and the fourth numerator is 1+3+9+27 = 40

and so forth.

Thus the fraction in 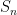S_{n} always has denominator 3^{n-1} and its numerator is the sum of the first n-1 squares of 3. There is a formula for that! You can get it by a careful application of the formula for the first n perfect squares. (If you look at the blog post I linked above, they work out something similar for the sum of the first n powers of 2). That’s the challenge! 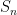and then you can find the limit of the S_{n}, which does exist: this series converges.

To be continued!

Homework:

• Review the examples, definitions and theorems discussed in class. (Not all of the examples are written up here, alas.)

• Do the WeBWorK on sequences: due by Sunday evening:do not wait to the last minute!

• I am also adding a short WeBWorK on series, due Sunday.

• Start working on the Test 2 redo problems if you choose to do them. Please pay careful attention to the instructions. In particular, the due date/time is firm.

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

Monday 23 October and Wednesday 25 October classes

(Wednesday after Test 2)

Topics:

• Taylor’s Theorem and the error term

• The Mean Value Theorem and Rolle’s Theorem (Ch. 3 section 3.2)

Here are my notes on the examples I used to illustrate these theorems:

MAT1575MeanValueThmRollesThmillustrations

You can also view this video on the MVT from PatrickJMT

We will use the Mean Value Theorem to prove the error term in Taylor’s Theorem, and then use the error term bound to figure out how many terms of the Taylor polynomial we would need to make the error be less than a specified amount.

Homework:

• Review the examples discussed in class

• Do the WeBWorK:

• There are no problems in the textbook assignment on the Mean Value Theorem, so make sure that you do that assignment on WeBWorK!

• For extra practice on Taylor polynomials you can do the problems p. 475 #5-20

• No quiz next time.

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

 

Test 2 review (updated, now with answers and some hints)

Test 2 is scheduled for the first hour or so of class on Wednesday 25 October.

Test 2 review self-tests here: MAT1575Test2Review 

You probably should allow 90 minutes per self-test: the test itself will not have quite so many problems in it!

Important note: there are some errors in a couple of the problems, which I did not catch before publishing these:

In Self-Test 1, problem 4, the integral should go from 7 to 9 (not 4 to 9)

In Self-Test 2, problem 2, there is a typesetting error: the integral should read \displaystyle \int \frac{x}{\sqrt{9x^{2}-1}}\textrm{d}x

Answers and hints are at the end of this post, after the “more”

Topics:
• Trigonometric integrals of the form $\int \tan^{m}(x) \sec^{n}(x)\textrm{d}x$, where m and n are positive integers.
• Trigonometric substitution, including completing the square to use it
• Partial Fractions, including repeated factors and irreducible quadratic factors
• Improper integrals and the two comparison theorems

Also make sure that you are familiar with the additional antiderivatives we found and added to our basic list:

MAT1575Integration-Formulas-Theorems-OurMethods-slideshow

 

It may be useful to fill out the Outline Summary of Integration Methods:

MAT1575OutlineSummaryOfIntegrationMethods

 

Here is a nice resource: an online, free Integral calculator. Don’t let it do everything for you, but it’s great for checking your work. This can be very helpful in locating errors since it shows step-by-step how it arrived at the integrals.

Continue reading →

Wednesday 18 October class

Topics:

• More on improper integrals: the Limit Comparison Theorem (and why it is more powerful than the direct Comparison Theorem); improper integrals when the interval of integration contains a vertical asymptote

• Introduction to Taylor polynomials

Notes to follow!

 

Homework:

• Review the examples we discussed in class. Especially make sure that you understand why direct comparison cannot be used in the example where I used limit comparison.

• Do the WeBWorK: there are two assignments due by Sunday evening, but do not wait to the last minute! And don’t forget to use Piazza to discuss! I have also extended the extra credit assignment on partial fractions.

• There will be a quiz next time: the topic will be improper integrals and the comparison theorems.

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

Monday 16 October class (updated)

I’ve started typing this up (as you can see, it’s got a lot of notes) but I’m getting error messages in some of the new things I’m trying to put in, so it’s incomplete. I’ll keep working on it, but wanted to give you these notes for now.

UPDATE: Here are the notes I have managed to get to work on this post. Some details remain for you to fill in! There is also a link to the Paul’s Notes page on L’Hôpital’s Rule which I highly recommend if you feel the urge to brush up on your skills! (Or even if you’ve totally forgotten what it is!)

Many of you have already started the WeBWorK, and I also extended the extra credit assignment: both are due Tuesday night!

There will be a quiz on partial fractions with either long division or irreducible quadratic factors (or both), plus one improper integral, next time.

 

Topics:

• Some homework problems from Partial Fractions 3

• Improper integrals (continued): the type where the interval of integration is infinite

Note: for working with improper integrals of this type, where we are taking limits as x\rightarrow \pm \infty, it is very useful to keep in mind that any time we take a limit of a rational expression whose numerator is a constant and the denominator goes to infinity, that limit will be 0. So for example

\displaystyle \lim_{x\rightarrow \infty}\left(\frac{1}{x^{p}}\right) = 0 for any p>0

\displaystyle \lim_{x\rightarrow \infty}\left(\frac{1}{e^{x}}\right) = 0

which means that \displaystyle \lim_{x\rightarrow \infty}\left(e^{-x}\right) = 0

and even

\displaystyle \lim_{x\rightarrow \infty}\left(\frac{1}{\ln(x)}\right) = 0

Also, we may have to use L’Hôpital’s Rule when we encounter the situation where the limit has one of the indefinite forms:

\frac{\infty}{\infty}, \frac{0}{0}, \infty - \infty, etc.

 

Here are examples I discussed: (some details omitted, you should be able to fill in the missing steps though!)

\displaystyle \int_{1}^{\infty}\frac{1}{x}\textrm{d}x = \lim_{b\rightarrow\infty}\left[\ln(x)\right]_{1}^{b} diverges to infinity because \lim_{b\rightarrow\infty}\left(\ln(x)\right) = \infty

 

\displaystyle \int_{-\infty}^{0}e^{x}\textrm{d}x = \lim_{a\rightarrow-\infty}\left[e^{x}\right]_{a}^{0} = 1 because \displaystyle \lim_{a\rightarrow -\infty}e^{a} = \lim_{x\rightarrow \infty}\left(e^{-x}\right) = 0

 

\displaystyle\int_{-\infty}^{\infty}\frac{1}{1+x^{2}}\textrm{d}x=\lim_{a\rightarrow-\infty}\left[\tan^{-1}(x)\right]_{a}^{0}+\lim_{b\rightarrow \infty}\left[\tan^{-1}(x)\right]_{0}^{b}

=0 - \left(-\frac{\pi}{2}\right) + \frac{\pi}{2} - 0 =\pi

Comment: I find the limits for the inverse tangent by considering the graph of tangent in the period between -\frac{\pi}{2} and \frac{\pi}{2}; as \tan(x) \rightarrow -\infty in this part of the graph, the angle x is approaching -\frac{\pi}{2}, and as \tan(x) \rightarrow \infty in this part of the graph, the angle x is approaching \frac{\pi}{2}.

You can find the indefinite integral for \int\frac{1}{1+x^{2}}\textrm{d}x either by remembering that \frac{1}{1+x^{2}} is the derivative of \tan^{-1}(x), or else by using a trig substitution x=\tan^{2}\theta.

 

Example using L’Hôpital’s Rule:

\displaystyle \int_{1}^{\infty}\frac{\ln(x)}{x^{2}}\textrm{d}x

Note: this is Example 194 on p. 336 in the textbook, done there in considerable detail. We end up using L’Hôpital’s Rule to find \displaystyle \lim_{b\rightarrow\infty}\frac{\ln(b)}{b}, which is an indefinite form of the type \frac{\infty}{\infty}.

 

A general rule for integrals involving powers of x in the denominator: this will be useful for comparison to prove whether or not other indefinite integrals converge.

Consider the improper integral \displaystyle \int_{1}^{\infty}\frac{1}{x^{p}}\textrm{d}x with p>0, p\neq 1.

What values of p will make it converge? When we integrate, we end up having to compute

\displaystyle \lim_{b\rightarrow\infty}\frac{b^{-p+1}}{-p+1}

This will go to 0 if the exponent is negative: otherwise, it will diverge to infinity.

So in order to have the integral converge, we need -p+1<0, which means that p>1.

 

We already saw that this type of integral diverges when p =1, so now we know the following:

\displaystyle \int_{1}^{\infty}\frac{1}{x^{p}}\textrm{d}x converges when p>1, and it diverges when 0 < p \le1.

 

Comparison Theorem:

Let f(x) and g(x) be functions such that both f(x) and g(x) are continuous on the interval [a, \infty)

and 0 \le f(x) \le g(x) for all x in [a, \infty)

Then:

• If \displaystyle \int_{a}^{\infty}g(x)\textrm{d}x converges, then also \displaystyle \int_{a}^{\infty}f(x)\textrm{d}x converges.

• If \displaystyle \int_{a}^{\infty}f(x)\textrm{d}x diverges, then also \displaystyle \int_{a}^{\infty}g(x)\textrm{d}x diverges.

 

Interpretation:

f(x) and g(x) have to be continuous on the given interval. Don’t forget to check this condition.

The condition 0 \le f(x) \le g(x) for all x in [a, \infty) means that both f(x) and g(x) are non-negative functions on the interval, and the graph of f(x) is squeezed in between the x-axis and the graph of g(x).

Now remember that the question of whether or not an improper integral of this type will converge, depends on how quickly the integrand goes to 0 as x\rightarrow\infty.

The first part of this theorem,

• If \displaystyle \int_{a}^{\infty}g(x)\textrm{d}x converges, then also \displaystyle \int_{a}^{\infty}f(x)\textrm{d}x converges,

is saying that g(x) goes to 0 “fast enough” that its integral converges. Since the graph of f(x) is squeezed between the graph of g(x) and the x-axis, that means that f(x) goes to 0 at least as fast as g(x) does, maybe faster. So the integral of f(x) will also converge.

The second part of this theorem,

• If \displaystyle \int_{a}^{\infty}f(x)\textrm{d}x diverges, then also \displaystyle \int_{a}^{\infty}g(x)\textrm{d}x diverges,

is saying that f(x) does not go to 0 “fast enough” for its integral to converge. Since the graph of f(x) is squeezed between the graph of g(x) and the x-axis, that means that g(x) goes to 0 no faster than f(x) does, maybe slower. So the integral of g(x) will also diverge.

(A picture may help. See the graphs on p. 340 of the textbook.)

 

Example: see Ex. 197 part 2 on p. 340 (to the end of the page).

I also discussed the convergence of \displaystyle \int_{1}^{\infty}\frac{1-e^{-x}}{x^{2}}\textrm{d}x.

Since 0\le e^{-x} <1 for x in the interval [1,\infty), the numerator 1-e^{-x} will always be a positive number less than 1 in that interval. So we can use comparison:

0\le \frac{1-e^{-x}}{x^{2}} \le \frac{1}{x^{2}} on [1,\infty)

We know from before that \displaystyle \int_{1}^{\infty}\frac{1}{x^{2}}\textrm{d}x converges, so it follows that \displaystyle \int_{1}^{\infty}\frac{1-e^{-x}}{x^{2}}\textrm{d}x converges.

 

General comment on this comparison theorem: The theorem can only tell you that a certain integral converges: it does not tell you what the value of that integral is. In the example I just worked, we know that \displaystyle \int_{1}^{\infty}\frac{1-e^{-x}}{x^{2}}\textrm{d}x converges, but the most we can say about its value is that \displaystyle \int_{1}^{\infty}\frac{1-e^{-x}}{x^{2}}\textrm{d}x\le\int_{1}^{\infty}\frac{1}{x^{2}}\textrm{d}x.

You may wonder why it is useful to know that something converges if we don’t know its actual value. One reason that it is useful to know this is that once we know that the integral converges, we can use numerical methods to estimate its value if all else fails. It is very dangerous to try to use numerical methods on an integral if we don’t know whether or not it converges!

Numerical methods are very important in applications (physics, etc) where many of the integrals we want to compute cannot be found explicitly even by the many methods you learn in this course!

 

Delayed posts (UPDATED)

 

UPDATE: I accidentally posted topics here which are actually for a different class! Sorry, I’m working on this today (Sunday) and will post a final version when all the editing is finished. I am also trying to re-post the resources which needed corrections.

 

The resources are still linked in the last post [corrected link] and here is the  Homework:

• Review the methods for integration by partial fractions when there is an irreducible quadratic factor, and the definitions of improper integrals when the integration interval is infinite

• Do the problems assigned in the Course Outline

for the partial fractions (second part)

• Do the WeBWork

• Here is some review on L’Hopital’s Rule (which we will need to use next time), and there are also practice problems with solutions included. [From Paul’s Notes]

• There will be a Quiz on Monday, the topics will be integrating by partial fractions, and there will be the possibility of) denominators which are not linear so you have to use trig substitution.