Wednesday 18 October class (to be updated)

Posted on October 18, 2017 by Sybil Shaver

Note: I am trying to find a way to display the synthetic division in this, but I want to post these notes already. I will update when I’ve found a way to do that.

Topics:

• review of homework problems on roots and factors

• Review of two methods for solving a quadratic equation (other than factoring and using the zero product property, which was mentioned last time), with a quick reminder that we define \sqrt{-1} = i.

The methods:

If the quadratic equation does not have a 1st degree (linear) term, it can be solved using the square root property:

x^{2} = c \implies x=\pm\sqrt{c}

 

Examples:
x^{2}-9 = 0 (note: this could also be solved by factoring)
x^{2} = 9
use the square root property:
x = \pm\sqrt{9}
x = \pm 3

x^{2}+16 = 0
x^{2} = -16
use the square root property:
x = \pm\sqrt{-16} = \pm\sqrt{-1}\sqrt{16}
x = \pm 4i

Any quadratic equation can be solved by putting it into the form

ax^{2} + bx + c = 0

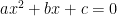
and using the quadratic formula

x = \frac{-b\pm\sqrt{b^{2} - 4ac}}{2a}

Even though this could always be used to solve a quadratic equation, it is usually better to use factoring or the square root property when you can do so. But when all else fails you can use the quadratic formula, and you need to memorize it – something I don’t say very often!

• Important theorems about roots and factors (see the notes below)

• Using all of this to find all of the roots of a polynomial, and/or a complete factorization of the polynomial over the complex numbers.

The important theorems about roots and factors: (don’t forget we had some other important theorems about roots, factors, and remainders last time)

The Fundamental Theorem of Algebra:

If p(x) is a polynomial of degree n\ge 1, then p(x) has at least one root in the set of complex numbers \mathbb{C}

In this theorem, it is important to remember that the complex numbers include the real numbers. The theorem is saying that every non-constant polynomial has at least one root, but you have to allow for the possibility that the root is not a real number. See the second example above where we used the square root property and found two imaginary roots.

A consequence of the Fundamental Theorem of Algebra:

The polynomial p(x) of degree n will have exactly n roots in \mathbb{C}, if we also count multiple roots according to their multiplicities.

Remember that a multiple root is a root whose factor appears more than once in the factorization of the polynomial.

 

If the polynomial p(x) of degree n \ge 1 has roots c_{1}, c_{2},\dots, c_{n}, then p(x) has a complete factorization of the form

p(x) = a(x-c_{1})(x-c_{2})\cdots(x-c_{n})

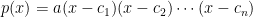
where a is the leading coefficient of p(x) (if the leading coefficient is not 1).

See the examples below.
There is one more theorem, which I will mention after the examples.

Examples:

Find all the roots of the polynomial, and use them to find a compete factorization of the polynomial.

[10.7 (a)] p(x) = 2x^{3} - 8x^{2} -6x + 36

Looking at this polynomial, we see that its degree is 3 so we are expecting it to have 3 roots. Also, there is a common factor of 2 in all the terms, so we will factor that out first:

p(x) = 2\left(x^{3} - 4x^{2} -3x + 18\right)

Now we can try to guess the roots by looking at the graph of p(x). From the graph it appears that there are roots at -2 and 3, and it also appears that 3 is a double root. Let’s verify that this is so, using synthetic division:

[I’ll fill this in later]

So we get the complete factorization (don’t forget the 2 which we factored out at the start!):

p(x) = 2(x+2)(x-3)^{2}

 

[10.7(b)] p(x) = x^{4} - 3x^{3} - 36x^{2} + 68x + 240

We see that this polynomial has degree 4, so we are expecting 4 roots. Also the leading coefficient is 1, so there will not be an additional numerical factor as there was in the previous example.

By looking at the graph, it appears that there are roots at -5, -2, 4, and 6. We can verify this by synthetic division:

[I will fill this in later]

So we have a complete factorization:

p(x) = (x+5)(x+2)(x-4)(x-6)

 

[10.7(c)] p(x) = x^{3} + 1

We see that this polynomial has degree 3, so we are expecting 3 roots. Also, the leading coefficient is 1.

By looking at the graph (or just guessing), it appears that there is a root at -1, but no other real number roots. We can use synthetic division to verify this and find out what to do next:

[I will fill this in later]

The quotient after dividing by x+1 is x^{2} - x +1, which cannot be factored by elementary methods. So we use the quadratic formula to find the remaining two roots, which are x = \frac{1}{2} \pm \frac{\sqrt{3}}{2}i.

Notice that these are complex conjugates – they are the same except that the imaginary parts have opposite signs. This is an instance of the last theorem for today, which I will give below.

So we have a complete factorization

p(x) = (x+1)\left[x-\left(\frac{1}{2} \pm \frac{\sqrt{3}}{2}i\right)\right]\left[x-\left(\frac{1}{2} \pm \frac{\sqrt{3}}{2}i\right)\right]

Here is the final theorem of the day:

If the polynomial p(x) has only real number coefficients, then any non-real complex roots will appear in conjugate pairs.

 

Homework: please note that the WeBWorK does not cover everything! There are other problems from the textbook you need to do.

• Review the examples and theorems discussed in class. Make especially sure that you understand the following:

The relationship between a root of a polynomial and the factor of the polynomial that the root corresponds to

How to verify a root of a polynomial (by substitution, or by division)

How to use the square root property correctly, and why it’s wrong to “square root both sides”

How to use the quadratic formula and simplify your results

• Do the following problems from the textbook:

In Session 10, Exercises 10.3(a-c) and 10.4(a-c and f-h). We will discuss the graphs in 10.4 next time.  Students may put their solutions to these problems on the board at the start of class next time: please make sure that you show us how you verified your roots! (It’s not enough to just say what you read off the graph! You must check that they actually are roots, either by substitution as the textbook does, or by synthetic or long division.)

• Do the WeBWorK: due by Sunday evening, but do not wait until the last minute! And don’t forget to make use of Piazza to discuss!

• Information and resources for next time will be posted soon. Please look for this and take a look at the resources before we meet.

• There will be a quiz next time: the topic will be using one root to find a complete factorization of a polynomial

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

This entry was posted in Uncategorized. Bookmark the permalink.