Blog

Eventually we will move the notes to Blackboard. For now adding the notes here:

CET3625_Lecture3

In the lesson 2 we discussed taking numerical derivatives using the finite difference method.

We considered the function y=x^2.  The task is to numerically calculate the first derivative by taking differences.

For example setting up an array for x :

x= [-3   -2  1  0  1  2  3]

with the step size

dx = (x(end)-x(1) )/(size(x,2)-1) = (3-(-3))/(7-1) = 6/6 = 1

we get the following array for the function y=x.^2

y = [9  4  1  0 1  4  9]

To compute the numerical central derivatives we take the difference between the  arrays that are shifted by two positions and divide by twice the step size. The factor 2 for the step size is because we shifted by two positions.

dydx =
( y(3:end)-y(1:end-2)  ) / (2*dx) =
(       [   1      0     1    4   9]
–    [  9      4     1     0   1]     ) / 2
=        [  -8  -4     0    4  8 ]    / 2
=        [   -4   -2    0   2  4]

which are the values of the first derivative of y for the corresponding values of x.

The array of dydx we got so far is two elements shorter than the array of y, it misses the first and the last element. To make both array the same size we add one additional element to the front and one to the back of dydx by simply extrapolation.

For example, we see that the difference between the last two elements of dydx is 4-2=2. Thus we add 2 to the last element to get to 6=4+(4-2).  Similarly we extend the beginning of dydx with -4+(-4 – (-2) ) =  -6. Thus we get

dydx = [ -6 -4 -2  0  2  4  6]

This corresponds to the expected result of dydx = 2x .

—————————————–

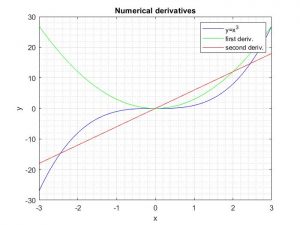
The task for the lesson was to compute the second derivative d2ydx for the function y=x.^3 , using the three point formula

d2ydx(i) =  ( y(i-1) – 2*y(i) + y(i+1) ) / (dx^2)

The formula is derived from first taking the one sided first differences

dydx(i+1) =  (  y(i+1)- y(i    ) )/dx
dydx(i) =      (  y(i)     – y(i-1) )/dx

and taking the difference of the differences above

d2ydx(i) =  (  dydx(i+1)-dydx(i-1) )/dx
(  (y(i+1)-y(i))-(y(i)-y(i-1))  ) / (dx^2)

Below is the starter code for the task, just missing the specification for d2ydx:

x = linspace(-3,3,61); 
dx = (x(end)-x(1))/(size(x,2)-1);
% Function y(x) definition
y = x.^3;

% First derivative
dydx = y(3:end)-y(1:end-2);
dydx = [(2*dydx(1)-dydx(2)) dydx (2*dydx(end)-dydx(end-1))]/(2*dx);

% Second derivative
d2ydx = FILL IN THE THE MISSING CALCULATION HERE
d2ydx = [(2*d2ydx(1)-d2ydx(2))   d2ydx   (2*d2ydx(end)-d2ydx(end-1))]/(dx^2);

% Plotting
plot(x,y,'b-'); hold on; plot(x,dydx,'g-'); plot(x,d2ydx,'r-'); 
xlabel('x');ylabel('y');
title('Numerical derivatives');legend('y=x^3','first deriv.','second deriv.'); 
grid on; grid minor; hold off;

Lecture slides from week 1 and week 2

1568247512-CET3625_Lecture1

1568435699-CET3625_Lecture2