Tried both integrating factors (because of the hint) and variation of parameters and I’m at a dead end. Did anyone approach these questions differently.
Problem 6
Getting the same answer with integrating factor method and variation of parameters
Author: Brian Enriquez (Page 4 of 5)
Problem 2
I don’t know where I’m making a mistake
Problem 3
I followed the hint too but still don’t know where I’m going wrong
Problem 7 and 8
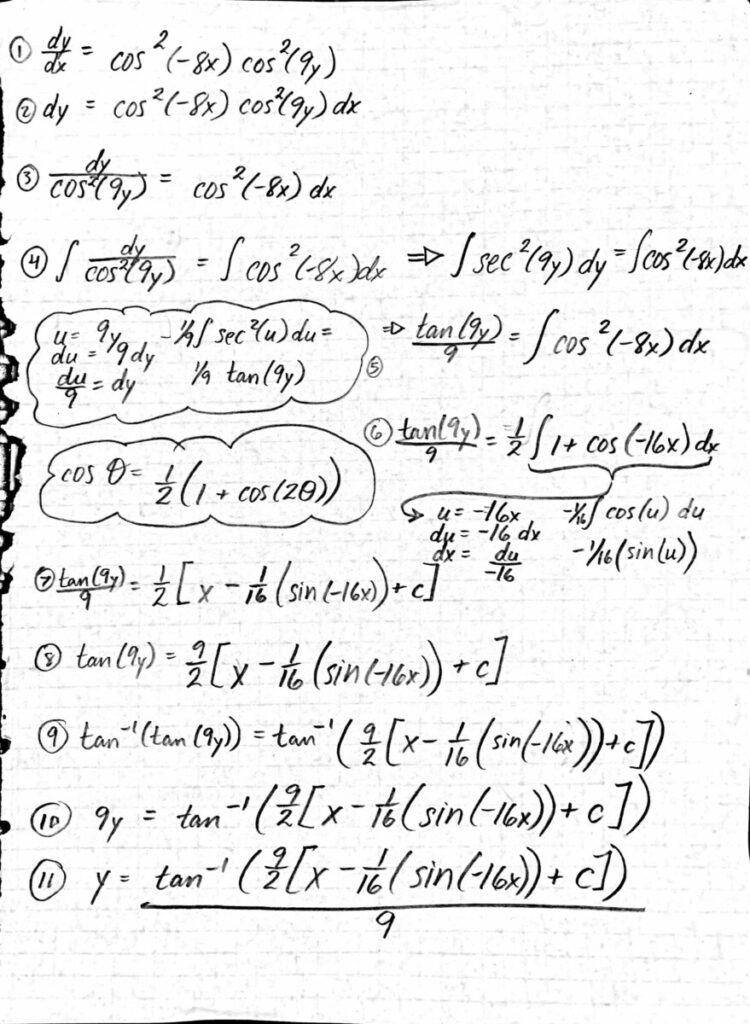
Anyone else knows what the hint means by “Use a substitute variable to replace y in order to make this DE separable”?
Practice Problem 1.2.2.E
Verify that the given is a solution to the ODE:
$y = \tan(\frac{x^{3}}{3}+c); y’ = x^{2}(1+y^{2})$
Solution:
$\frac{d}{dx}(\tan(\frac{x^{3}}{3}+c)) = x^{2}\sec^{2}(x)$
Recall that ,
$\tan^{2}(\theta)+1 = \sec^{2}(\theta)$
Thus,
$(1+y^{2}) = (1+tan^{2}(\frac{x^{3}}{3}+c)) = \sec^{2}(\frac{x^{3}}{3}+c))$
Therfore,
$y’ = x^{2}(1+y^{2}) = x^{2}(1+tan^{2}(\frac{x^{3}}{3}+c)) = x^{2}\sec^{2}(x)$
$y$ is a solution for $y’$ for all all real numbers ($\mathbb{R}$) excluding when $\frac{x^{3}}{3}+c = 0$
Practice Problem 1.3.7
Recent Comments