A few people asked about tutoring after today’s test. Here’s an updated schedule for the Atrium Learning Center (on the ground floor of the Library Building) as well as the schedule for tutoring from the math department. I’ll also attach a flyer for a note-taking workshop this Thursday that may be useful for you. (Sorry for the blurry pictures…my phone is old and the camera lens is super scratched!)
Category: Uncategorized (Page 3 of 4)
Hey guys, is it just me or are there a lot of questions on the trig sub webwork that require partial fraction decomposition(like problem 10 and 11)? I’m not really sure how to do those two without partial fraction decomposition being as there’s no radical in the problem.

Due to t not being a real # when t > 1, this integral is invalid because there cannot be negative under the radical.
 Basic Trig identity Function used in Problem
Basic Trig identity Function used in Problem
 Substitution used while the limit of bounds are changed to better use integration
Substitution used while the limit of bounds are changed to better use integration
I’ve received a few questions about what to expect on Test #1. Here are some answers.
- There will be 10-15 questions total.
- Questions will be graded just like quiz questions: total of 10 points per question including 1 point for style and 3 for checking antiderivatives by differentiating (where appropriate): shorter questions will be worth 5 points each.
- No formula sheets are allowed. You must memorize the relevant trig identities as well as derivatives and antiderivatives.
- You must show all your work. If no work is shown but an answer is given without justification, a report will be filed with the Academic Integrity Committee.
- You may use a calculator, but you may not use any other devices (you may not use your phone’s calculator).
- You will have the whole class period but time will be an issue. Make sure you complete your practice problems several times so that you can complete them quickly.
- When you are applying a particular integration technique, state which one it is you are applying.
This week I’ll be in my office (probably!) around 11:30 or 12:00 noon; check in at N707.
Tomorrow (Thursday) I’ll be in my office N707 from 12:00 noon to about 12:30.
I wanted to return to the example we were considering in class today, before too much time passes and we forget where we were.
Recall, we were trying to evaluate the integral $\int \frac{\sqrt{x^2-9}}{x}dx$. To do so, we tried making a substitution where $x = 3 \sec(\theta)$. In order to make this substitution, we used $x = 3 \sec(\theta)$ to create a dictionary that would take us from an integral in terms of $x$ to an integral in terms of $\theta$.
We saw that if $x = 3 \sec(\theta)$, then (after a little work) $\sqrt{x^2-9} = 3 \tan(\theta)$ and $dx = 3 \sec(\theta) \tan(\theta)d \theta.$
This means that $\int \frac{\sqrt{x^2-9}}{x}dx = \int \frac{3 \tan(\theta)}{3\sec(\theta)}3\sec(\theta)\tan(\theta)d\theta.$
After simplifying, this is equal to $3\int \tan^2(\theta)d\theta$.
This is how far we got in class. The point is that this is an integral we know how to evaluate.
To continue, $3\int \tan^2(\theta)\d\theta = 3 \int(\sec^2(\theta) – 1)d\theta = 3(\tan(\theta) – \theta) + C.$
To finish, we have to go back to our dictionary to write our answer in terms of $x$ instead of $\theta$. Remember, $x = 3 \sec(\theta)$, which means that $\frac{x}{3} = \sec(\theta)$. We have a $\theta$ to replace AND a $\tan(\theta)$ to replace.
To replace the $\tan(\theta)$ we don’t have to get $\theta$ by itself. We use $\frac{x}{3} = \sec(\theta)$ to label the sides of a right triangle. Draw a right triangle and label one of the acute angles by $\theta$. Since $\sec(\theta)$ is defined as the length of the hypotenuse over the length of the adjacent side, we can label the hypotenuse by $x$ and the side adjacent to $\theta$ by $3$. We can use the Pythagorean theorem to find the length of the side opposite to $\theta$: it’s $\sqrt{x^2-3}$. Then the $\tan(\theta)$ term in our answer is opposite over adjacent, which is $\frac{\sqrt{x^2-3}}{3}$.
To replace $\theta$ we do have to get $\theta$ by itself. We apply $\sec^{-1}$ to both sides of the equation $\frac{x}{3} = \sec(\theta)$ to get $\sec^{-1}(\frac{x}{3}) = \theta$.
This means our final answer is:
$\int \frac{\sqrt{x^2-9}}{x}dx = 3(\tan(\theta) – \theta) + C = 3(\frac{\sqrt{x^2-3}}{3} – \sec^{-1}(\frac{x}{3})) + C
= \sqrt{x^2-3} – 3\sec^{-1}(\frac{x}{3}) + C$.
A few people asked during class, “Where does $x = 3 \sec(\theta)$ come from?” That’s a tricky question to answer, because it doesn’t really *come from* anywhere. But we see from this example, that by making this substitution, we’re able to evaluate the integral. In some sense it *comes from* the Pythagorean identity $\tan^2(\theta) = \sec^2(\theta) – 1$.
In general, to make a trigonometric substitution:
- if you see $x^2 – a^2$ let $x=a\sec(\theta)$,
- if you see $a^2 – x^2$ let $x=a\sin(\theta)$,
- if you see $x^2 + a^2$ let $x=a\tan(\theta)$.
This should be enough for you to get a solid start on the Trigonometric Substitution Webwork set, which is due on March 1.
Hi,
my name is Elijah Rickman. This is my third year attending City Tech, my major is Mechanical Engineering. I chose this major because of my interest in cars. After I graduate, I want to pursue a career in the automotive field.





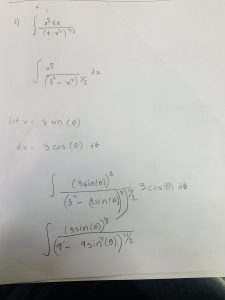






Recent Comments