Here’s the link to the Desmos graph we used to convince ourselves the derivative of 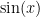 is
is 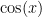 in class today.
in class today.
Also, your next WebWork set is due next Thursday night, October 15. (Usually WebWork is not due on Thursdays, but next week there’s no class on Monday, hence this change.)
This WebWork set–Derivatives-ProductQuotient–contains one problem that you won’t officially know how to complete yet. For now, you can skip #6. In class on Wednesday, we’ll see what the derivative of  is. Some of the later questions on the set involve using a combination of the product rule and the quotient rule. They can be a little tricky at first, so try them as soon as you can. We can go over any problems in class or in office hours on Wednesday.
is. Some of the later questions on the set involve using a combination of the product rule and the quotient rule. They can be a little tricky at first, so try them as soon as you can. We can go over any problems in class or in office hours on Wednesday.
I haven’t updated the due date for the set Derivatives-Trigonometric yet, because there are still a few techniques you need for some of the problems that you haven’t officially seen yet. But after today’s class, you can probably solve about half of the problems on this set. It’s a good idea to take a look at those problems now. (It should be clear which ones they are.)



