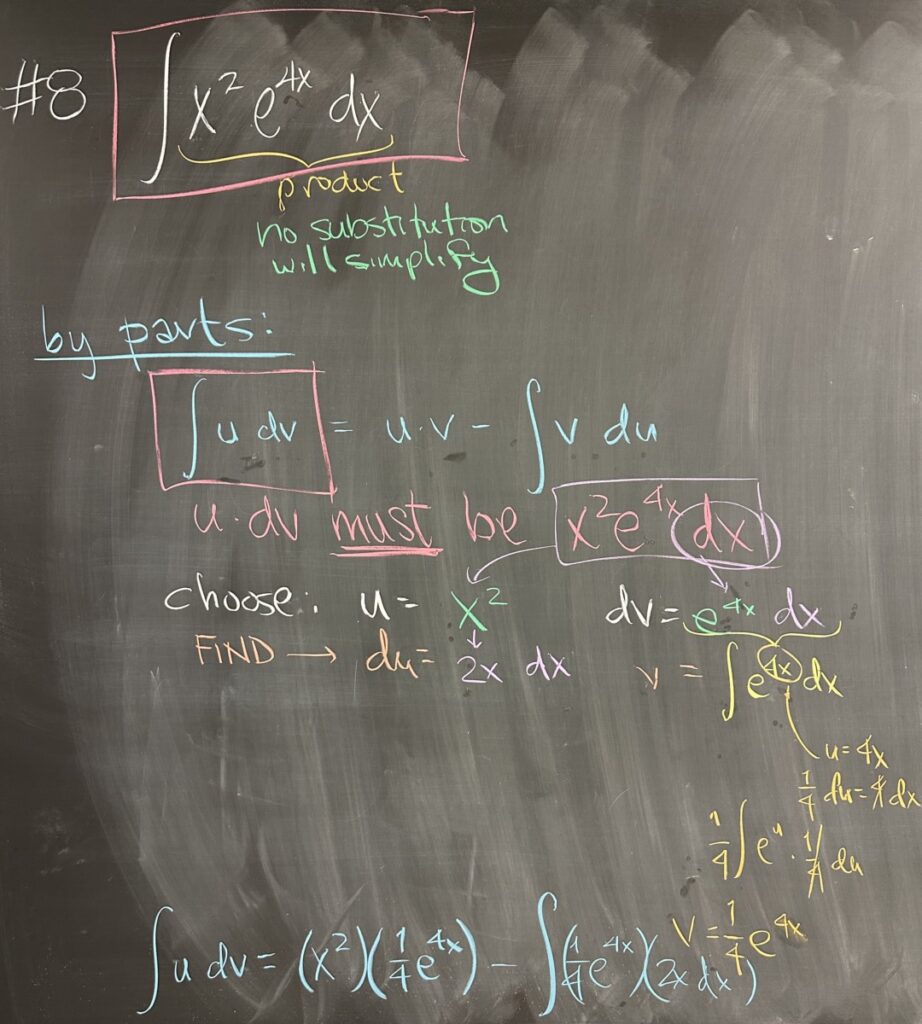
Instead of having a quiz today, we discussed a few problems from Thursday’s exam. The first problem we looked at was the indefinite integral: \(\int x^2 e^{4x}\,dx\). It is crucial to develop an intuition for the choice between u-substitution and integration by parts. This integral does not have a simplifying u-substitution, which can be difficult to determine if you haven’t been practicing your antiderivative skills on the homework.
The reason I chose this problem for discussion is because I saw some students struggling with the choice of how to break up \(x^2 e^{4x}\,dx\) into \(u\) and \(dv\). The product of \(u\) and \(dv\) must be \(x^2 e^{4x}\,dx\). Again, this choice is easier with practice. We choose \(u = x^2\) because \(du = 2x\,dx\) brings us closer to a factor that is constant. The remaining factors must then be \(dv = e^{4x}\,dx\).
Remember that \(v\) is the antiderivative of \(dv\), and as such, sometimes u-substitution is necessary for this step.
We did not finish this problem completely, but the next step would be to again apply integration by parts to bring that \(2x\) down to a constant factor \(2\).
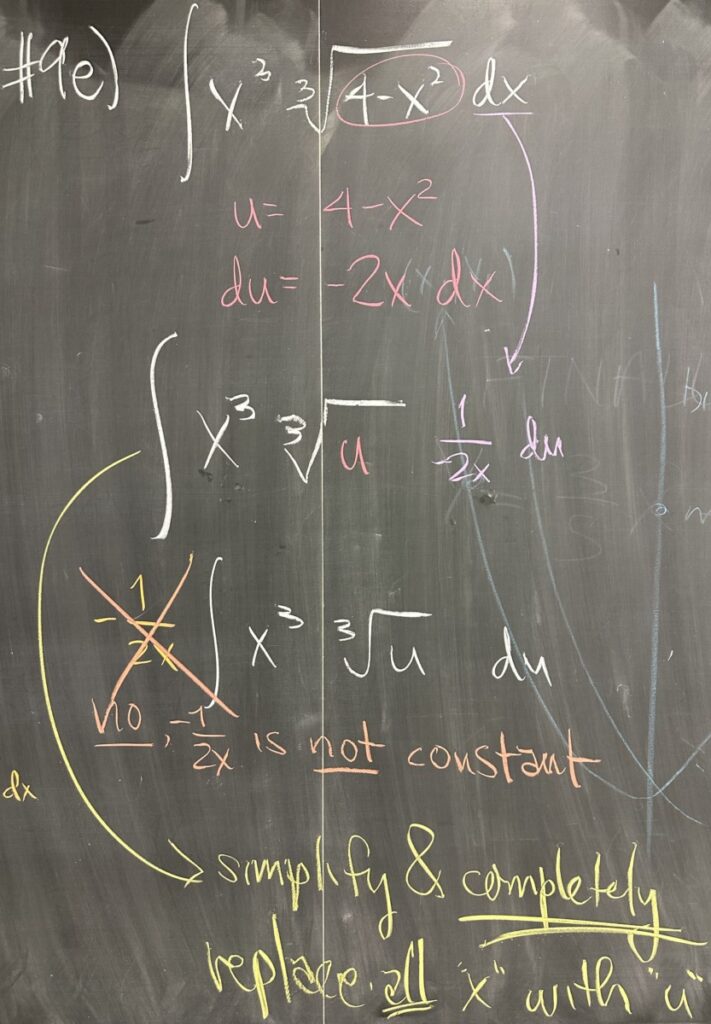
The next exam problem was chosen because I saw some substitution work that was incorrect. When substituting, for example, \(u = 4-x^2\) we get \(du = -2x\,dx\). While it is okay to solve for \(dx = -\frac{1}{2x}\,du\), we must make sure to replace ALL of the \(x\) with \(u\) before we continue with the antiderivative.
Furthermore, with this strategy, it is not okay to factor out \(-\frac{1}{2x}\) from the antiderivative. This is due to the presence of \(x\) in the factor — only *constant* factors may be pulled outside of the integral. This means it would be okay to factor out \(-\frac{1}{2}\), but \(\frac{1}{x}\) must remain part of the integral. Combining the product of \(\frac{1}{x}\) with \(x^3\), we get \(x^2\).
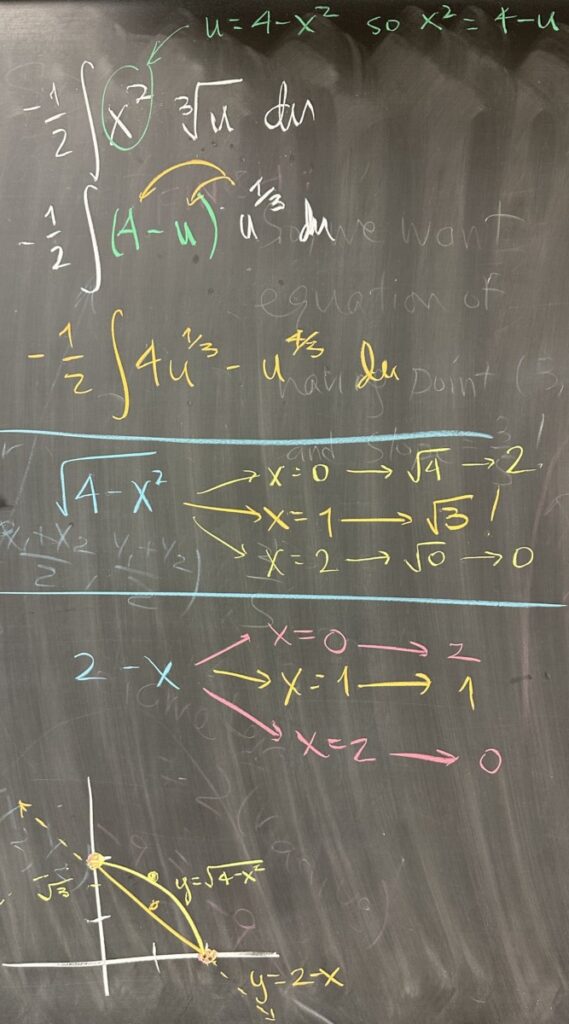
The result of the substitution is then completed by replacing \(x^2 = 4 – u^2\) to get \(\int (4-u^2)\sqrt[3]{u}\,du\). In order to find antiderivative of this product, we have to rewrite the product using the distributive property (as well as using the exponential form of the radical \(\sqrt[3]{u} = u^\frac{1}{3}\)).
I was asked about a hypothetical situation, so please note that we switched to looking at the square root (instead of the cube root) of \(4 – x^2\). It may be tempting to take the square root of the two squares, except that exponents (radicals are fractional exponents) cannot be distributed over sums or differences.
We then look at the behavior of \(\sqrt{4-x^2}\) in comparison to \(2 – x\). The first has a graph that looks like the upper-half of a circle (with radius two and centered at the origin); and the second is a line (with y-intercept \((0,2)\) and slope \(-1\)). These two clearly cannot be equivalent!
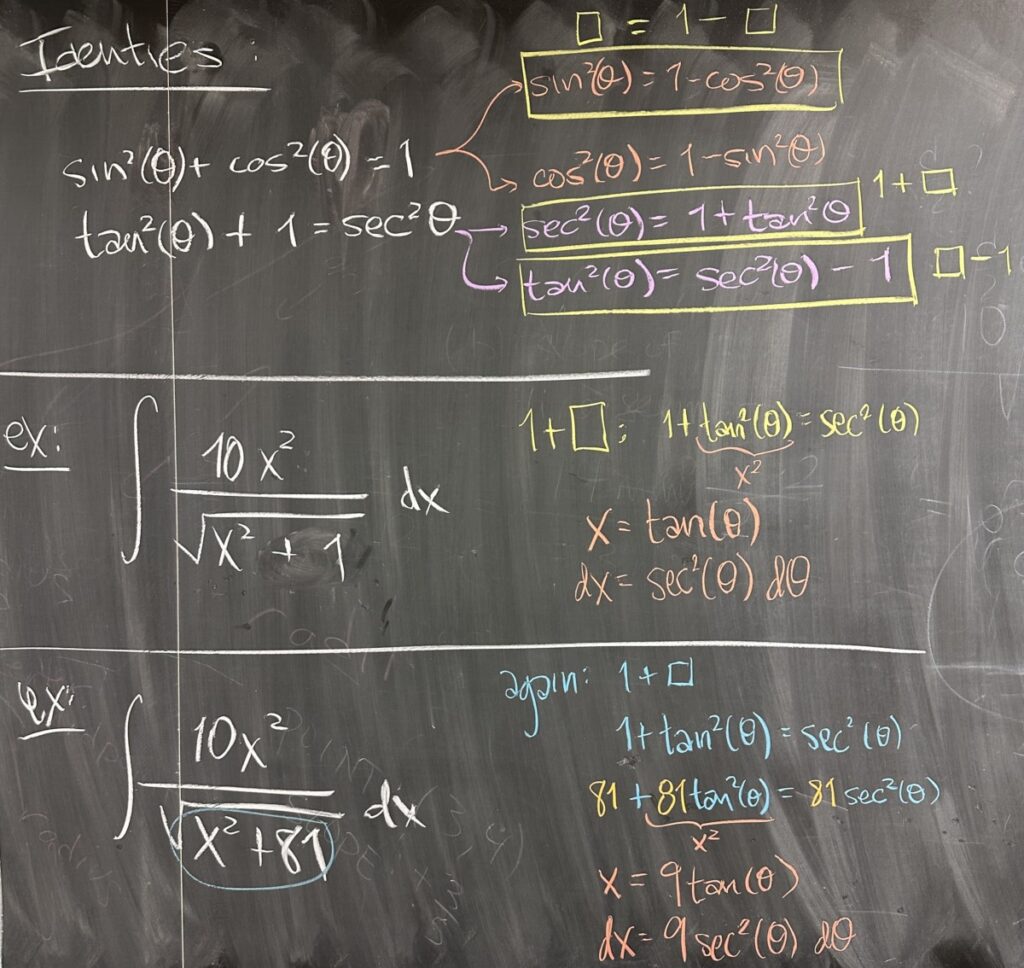
Moving on to the main topic for today’s lesson, we start with a foundational observation about the Pythagorean Identities for sine, cosine, tangent, and secant. We found three distinct patterns in these identities. One sum: \(1 + \square\); and two differences: \(1 – \square\) and \(\square – 1\). We will be looking for these patterns as a sign to use trigonometric substitution — and moreover, the specific pattern that we find will help us decide on the substitution we will use.
Note here that because sums are commutative, the sum pattern may appear in either order and they are interchangeable: \(1 + \square = \square + 1\).
We then look at how these patterns may appear in various integrals. In the first, \(\int\frac{10x^2}{\sqrt{x^2+1}}\,dx\), we recognize the \(\square + 1\) pattern (which corresponds to \(\tan^2(\theta)+1\)). In this pattern: \(x^2 + 1\), the replacement for \(x\) is \(\tan(\theta)\).
In the second example, instead of \(x^2 + 1\) we see \(x^2 + 81\). The pattern is still the same, except we need to convert \(\tan^2(\theta) + 1\) to get \(81\) as our constant. By multiplying the Pythagorean Identity by \(81\) (on both sides, of course), we get \(81\tan^2(\theta) + 81 = 81\sec^2(\theta)\). In order to use this version of the Pythagorean Identity, we need \(x^2 = 81\tan^2(\theta)\), which means using \(x = 9\tan(\theta)\).
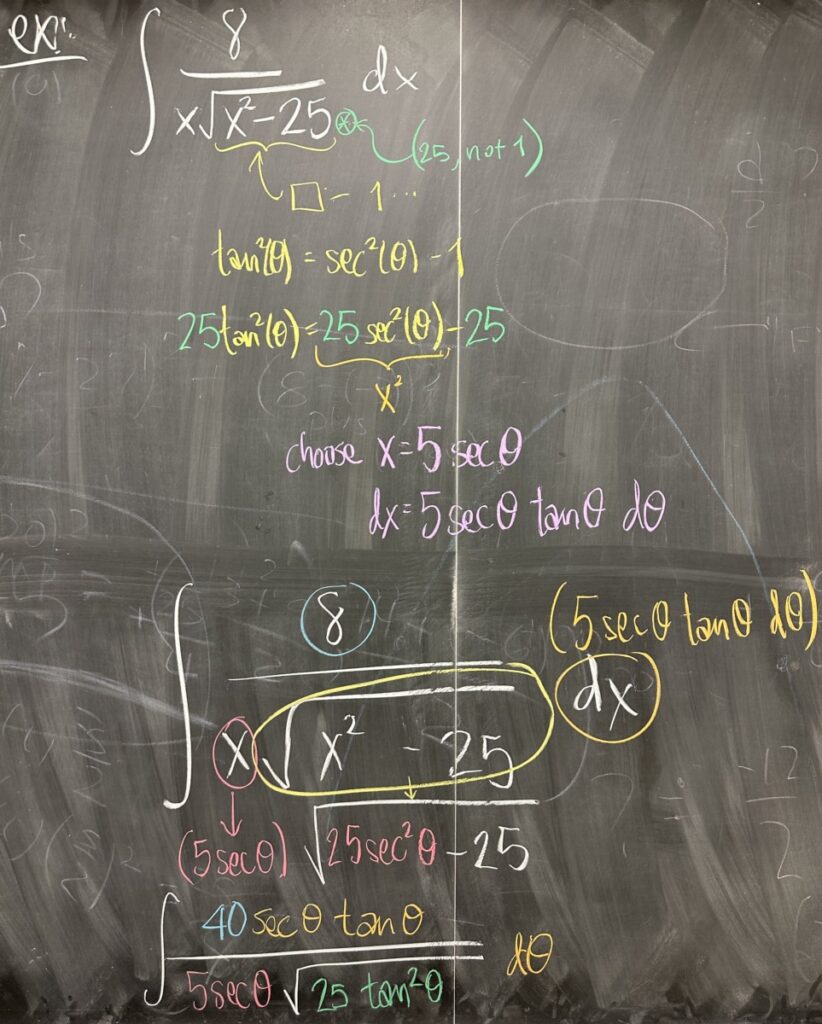
Next we turn to an example that has a different pattern than the first two: \(x^2 – 25\). This pattern is \(\square – 1\), which corresponds to \(\sec^2(\theta) – 1\); but instead of \(1\), we have \(25\). Applying the same strategy as in the previous example, we multiply the Pythagorean Identity on both sides by \(25\) to get \(25\sec^2(\theta) – 25 = 25\tan^2(\theta)\). In order to pull off this substitution, we need \(x^2 = 25\sec^2(\theta)\), which means we substitute \(x = 5\sec(\theta)\).
As with all substitutions, we must also substitute \(dx\). So from \(x\) we compute \(dx = 5 \sec(\theta)\tan(\theta)\,d\theta\).
After replacing all instances of \(x\) and \(dx\) we have: \[\int\frac{8\left(5\sec(\theta)\tan(\theta)\right)}{5\sec(\theta)\sqrt{25\sec^2(\theta) – 25}}\,d\theta = \int\frac{40\sec(\theta)\tan(\theta)}{5\sec(\theta)\sqrt{25\tan^2(\theta)}}\,d\theta \]
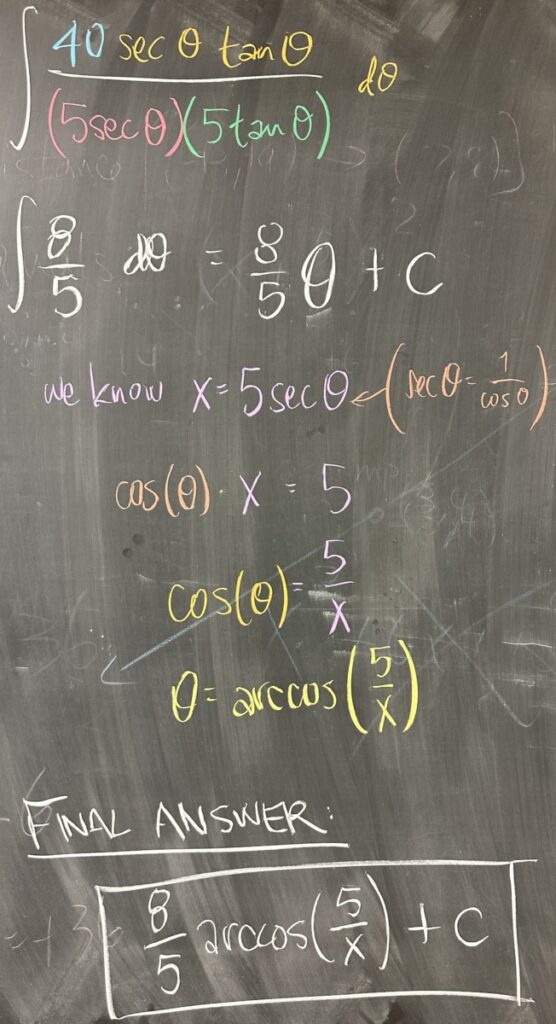
This fraction ends up simplifying to be \(\int\frac{8}{5}\,d\theta\). The integral is straightforward: \(\frac{8}{5}\theta + C\). In order to turn \(\theta\) back to \(x\), we must solve \(x = 5\sec(\theta)\) for \(\theta\): \(\sec(\theta) = \frac{x}{5}\), so \(\cos(\theta) = \frac{5}{x}\), and finally \(\theta = \arccos\left(\frac{5}{x}\right)\).
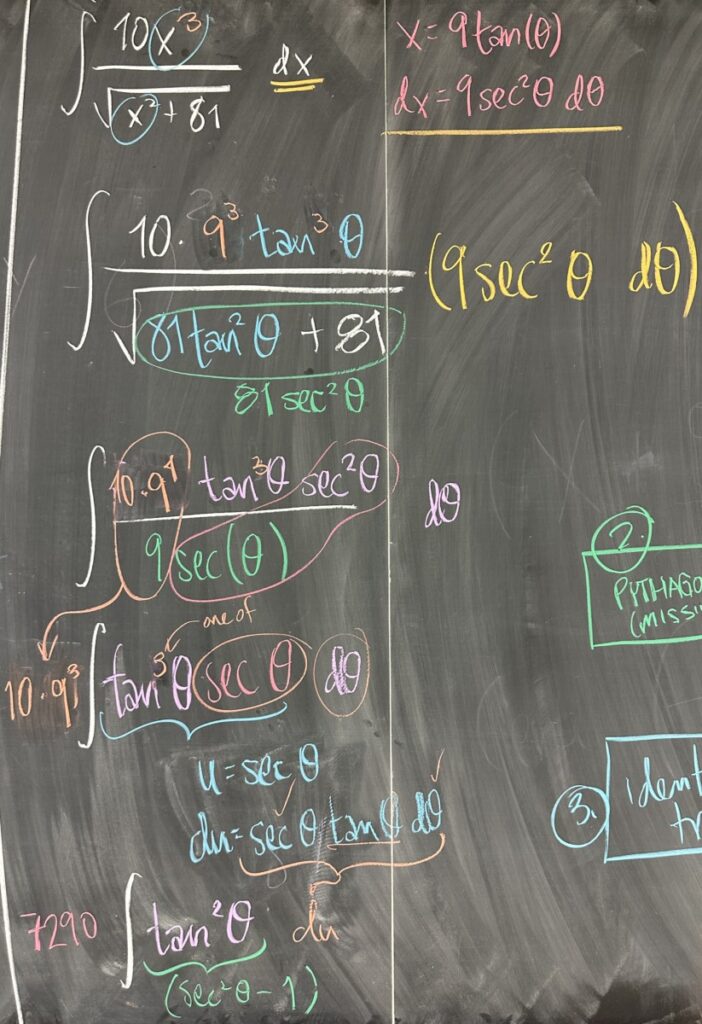
In the next example, we return to the “sum” identity pattern. Seeing \(x^2 + 81\), we plan to substitute \(x = 9\tan(\theta)\) and its counterpart \(dx = 9\sec^2(\theta)\,d\theta\). After making the substitutions for \(x\) and \(dx\) we have: \[\int\frac{10\left(9\tan(\theta)\right)^3}{\sqrt{81\tan^2(\theta) + 81}}\left(9\sec^2(\theta)\right)\,d\theta = 10 \cdot 9^3\int\frac{\tan^3(\theta)\sec^2(\theta)}{\sqrt{81\sec^2(\theta)}}\,d\theta\]
We can then reduce the square root in the denominator: \(9\sec(\theta)\), and further reduce a factor of \(\sec(\theta)\) and a factor of \(9\) with the coefficient. \[7290\int\tan^3(\theta)\sec(\theta)\,d\theta\]
This integral requires a substitution and more application of the Pythagorean Identity: \(\tan^2(\theta) = \sec^2(\theta) – 1\). By choosing \(u = \sec(\theta)\) and its counterpart \(du = \sec(\theta)\tan(\theta)\,d\theta\), we complete the substitution:\[\int7290\int\tan^3(\theta)\sec(\theta)\,d\theta = 7290\int (u^2 – 1)\,du\]
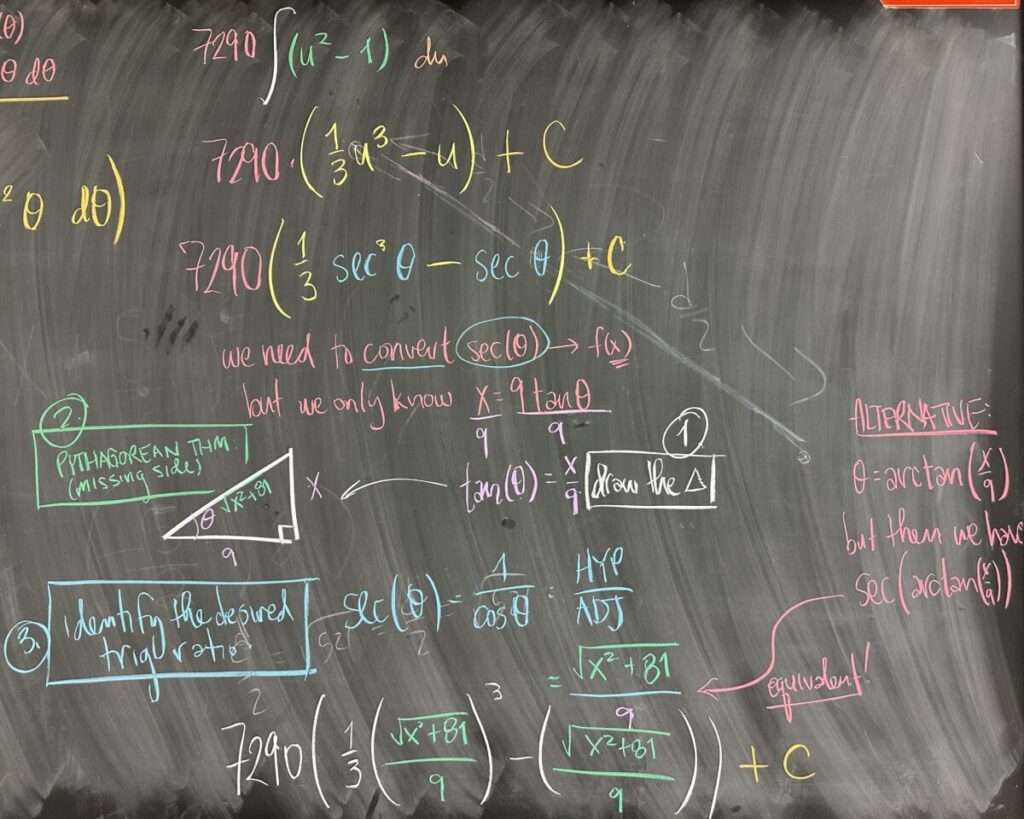
All that is left is to take the antiderivative, and then unravel all of our substitutions: \[7290\int(u^2-1)\,du = 7290\left(\frac{1}{3}u^3 – u\right) + C = 7290\left(\frac{1}{3}\sec^3(\theta) – \sec(\theta)\right) + C\]
We must then find a way to replace our instances of \(\sec(\theta)\) with some equivalent function of \(x\). The only relationship we have between \(x\) and \(\sec(\theta)\) is \(x = 9\tan(\theta)\). We are going to use the geometry of right triangles so we then solve for the trig ratio, rewriting our relationship as \(\tan(\theta) = \frac{x}{9}\).
We must interpret this relationship as \(\theta\) being an angle in a right triangle, with tangent ratio \(\frac{x}{9}\). This means having an opposite leg with length \(x\) and an adjacent leg with length \(9\). This leaves the hypotenuse unknown, but we know the Pythagorean Theorem applies to all right triangles, and so the hypotenuse must have length \(\sqrt{x^2 + 81}\).
Now that we know the lengths of all three sides of the right triangle, we can determine all six trig ratios for \(\theta\). We only need to find \[\sec(\theta) = \frac{\text{hypotenuse}}{\text{adjacent}} = \frac{\sqrt{x^2 + 81}}{9}\]
Finally, we substitute \(\sec(\theta)\): \[7290\left(\frac{1}{3}\left(\frac{\sqrt{x^2 + 81}}{9}\right)^3 – \left(\frac{\sqrt{x^2 + 81}}{9}\right)\right) + C\]




Recent Comments