See below for a guide to the various WebWork sets on exponential and logarithmic functions. We spent most of class on Mon Nov 30 doing examples from these WebWork sets, so you can also see the recording of that class session on Blackboard, and/or the whiteboard for that class.
Contents
“Exponential Functions – Graphs”:
This is an introduction to exponential functions, i.e., functions of the form
f(x) = A*Bx
and their graphs. We discussed the basic shapes of these graphs for various values of the “base” B in class. You should be able to do these exercises with the help of Desmos. One important feature of exponential functions to remember is:
f(0) = A*B0 = A
so the y-intercept of any exponential function is at (0, A).
Example: Exponential Functions – Graphs: Problem 6
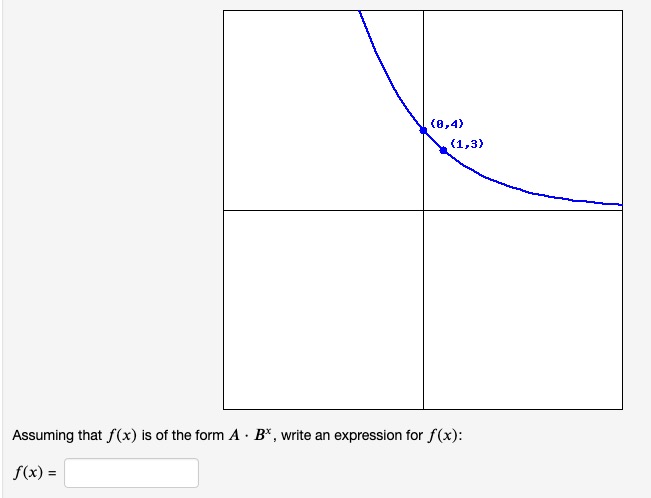
Note that since the graph slopes down from left to right, we know that the base B has a value between 0 and 1, i.e., 0 < B < 1.
Here the given y-intercept (0,4) gives us the value of the coefficient A:
f(0) = A*B0 = A = 4
and then we can use the fact that (1,3) is on the graph to solve for the base B. Since (1,3) is on the graph, f(1) = 3, giving us the equation:
f(1) = A*B1 = 4*B = 3
and therefore B = 3/4. Thus:
f(x) = 4*(3/4)x
Extra credit: Problems 8 & 9
“Logarithmic Functions – Graphs”
This introduces logarithmic functions and their graphs as the inverses of the exponential functions. In particular, many of these exercises discuss the domain, the vertical asymptote, and the x-intercept of various log functions. Read the text of Problems 1 & 3 carefully (which we discussed in class), and then use those ideas together with Desmos to work through the other exercises.
Example: Consider the function f(x) = log3 (-3x – 4).
Domain: Any log function can only take positive values as inputs (see the text of Problem 1!), and so the domain of this function is -3x – 4 > 0, i.e., x < -4/3.
x-intercept: To find the x-intercept, we need to solve f(x) = log3 (-3x – 4) = 0.
This occurs when -3x – 4 = 1, i.e., at x = -5/3. So the x-intercept is at (-5/3, 0).
Asymptote: Any log function has a vertical asymptote where the input value is 0, so in this case where -3x – 4 = 0, i.e., x = -4/3.
Extra credit: Problems 6 & 7
“Logarithmic Functions – Equations”
This set uses the fact that the definition of the log function y = logb(x) as the inverse of the exponential function with base b means
y = logb(x) is equivalent to by = x
Use this to rewrite the various logarithmic equations in the exercises as exponential equations!
Extra credit: Problems 5 & 6 (these exercises use the logarithmic properties, which are covered in the “Logarithmic Functions – Properties” set; so you may want to do that set first!)
“Logarithmic Functions – Properties”
This set introduces and applies the basic logarithmic properties. Refer to the textbook (Ch 14, specifically pp199-201) or the first part of Lesson 14 for a list of the basic log properties (which you have to give in Problem 1), and a lot of similar examples. See also the whiteboard for some examples we did in class.
“Exponential Functions – Equations”
This set involves using logarithms to solve exponential equations (i..e, equations in which the variable in the exponent). The key idea is to take the logarithm of both sides of a given equation, and to use the log properties “to bring the exponent down in front”. Refer to the textbook (Sec 14.2) and the latter part of Lesson 14 for examples. See also the whiteboard for some examples we did in class.



Leave a Reply