If you would like to review the material that’s on Quiz #3, I recommend that you study Example 10.7 in the textbook–especially 10.7(a):
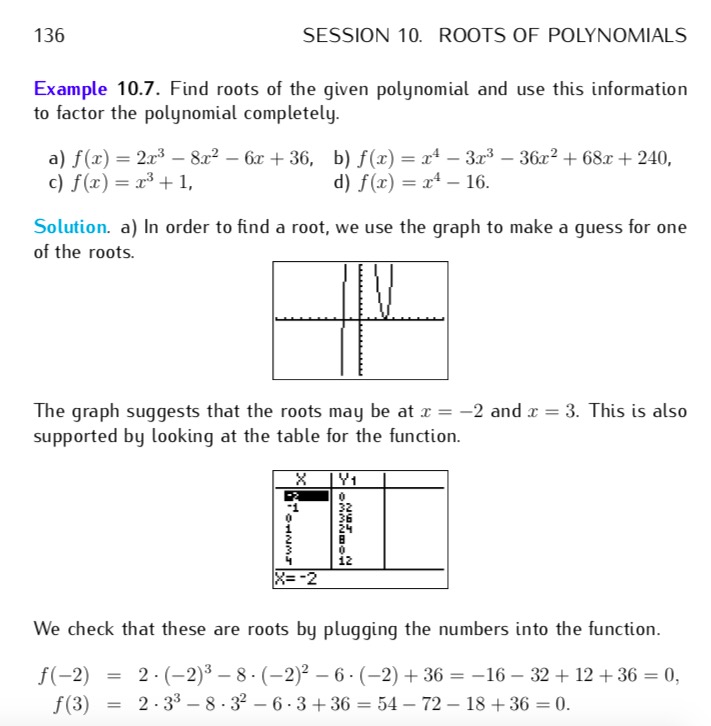
In this example, you are presented with various polynomials and asked to find the roots, and use them to factor the polynomial completely.
Let’s take a closer look at the polynomial in 10.7(a): the cubic polynomial
f(x) = 2x3 – 8x2 – 6x + 36.
How do we find the roots of this cubic? As you can see in the textbook explanation, we can start by looking at the graph! Here’s a nicer version of the graph I created in Desmos:

Note that I factored the common factor of 2 out of the polynomial. That makes the algebra a little bit simpler going forward…
Now, as the textbook explains as well, from looking at the graph it seems like x = -2 and x = 3 are roots. But to be sure we should check algebraically, i.e., by evaluating f(-2) and f(3), as they do in the textbook. The algebra is (just a bit) simpler with the 2 factored out:
f(3) = 2*( 3^3 – 4*(3^2) – 3*3 + 18) = 2*(27 – 36 – 9 + 18) = 2*0 = 0
Now how can we use the roots to factor the polynomial? That’s where the “Factor Theorem” comes in. It’s stated in Sec 8.2 of the textbook (read that section!); here is a statement via wikipedia:
“The factor theorem states that a polynomial 



Note that k here represents a constant value for the input variable x.
So in our example, since we know that k = 3 is a root of f(x), therefore we know that (x – 3) is a factor of f(x)! Similarly, since k = -2 is a root of f(x), we know that (x – (-2)) = (x + 2) is a factor of f(x).
How can we use that information to actually factor f(x)? By long division! In this case, we would set up long division in order to compute either
f(x) ÷ (x – 3)
or
f(x) ÷ (x + 2)
In the textbook (see the bottom of p136) they carry out the long division f(x) ÷ (x-3) to show that
f(x) = (x – 3)(2x2 – 2x – 12)
Here’s the long division for (x3 – 4x2 – 3x + 18) ÷ (x + 2) (I’m leaving out the factor of 2 from f(x) for the long division, but then put it back in at the bottom when factoring f(x)):
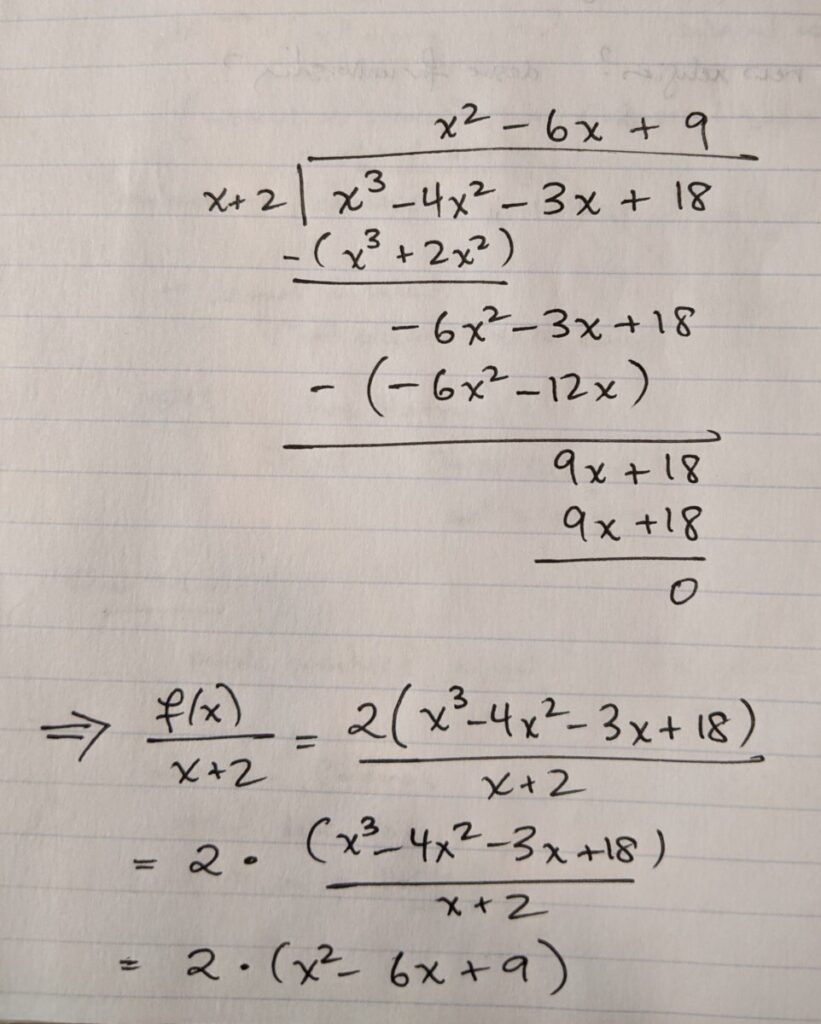
Therefore, we conclude that
f(x) = 2(x + 2)(x2 – 6x + 9)
and in this case we can factor the quadratic to get:
f(x) = 2(x + 2)(x2 – 6x + 9) = 2(x + 2)(x – 3)(x – 3) = 2(x + 2)(x – 3))2
This shows that the only roots of f(x) are x = -2 and x = 3 (where the latter is a root of multiplicity 2), and thus (as the Desmos graph seemed to show, but which we have now proved algebraically): the only x-intercepts of the graph are at (-2, 0) and (3,0).
Also note that we can easily find the y-intercept of the graph by computing f(0):
f(0) = 2*( 0^3 – 4*(0^2) – 0*3 + 18) = 2*(18) = 36
i.e., the y-intercept is at (0, 36), again as indicated by the Desmos graph.



Note: I just updated this post with the polynomial long division, and showed how that allows us to get to the fully factored form (and hence all the roots) of the given polynomial. Let me know if you have any questions!
Also a reminder that the “Rational Functions – Domains” WebWork set is due tonight, so finish that first if you haven’t already, and then complete the quiz (due Sunday).