Hi everyone! Read through the material below, watch the videos, and send me your questions.
Lesson 13: Exponential and Logarithmic Functions
Topic: This lesson covers Chapter 13 in the book, Exponential and Logarithmic Functions.
WeBWorK: There are two WeBWorK assignments on today’s material:
Exponential Functions - GraphsandLogarithmic Functions - Graphs.
Lesson Notes (Notability – pdf):
This .pdf file contains most of the work from the videos in this lesson. It is provided for your reference.
Exponential Functions and their Graphs
We’ve been living in the world of Polynomials and Rational Functions. We now turn to exponential functions. These functions are “very natural” – that is, they show up in the real world – but they are also more complicated than Polynomial and Rational functions (for example, an exponential function grows more quickly than any Polynomial)
The spread of coronavirus, like other infectious diseases, can be modeled by exponential functions.
Definition. An exponential function is a function of the form $f(x)=c\cdot b^x$, where $b$ and $c$ are real numbers and $b$ is positive ($b$ is called the base, $x$ is the exponent).
Example 1 (Textbook 13.2): Graph the exponential functions $f(x)=2^x, g(x)=3^x, h(x)=10^x, k(x)=\left(\frac{1}{2}\right)^x, l(x)=\left(\frac{1}{10}\right)^x$.
Now let’s see what happens when we change the number $c$ in $y=c\cdot b^x$.
Example 2 (Textbook 13.6): Graph the exponential functions
a) $y=2^{x}, \quad$ b) $y=3 \cdot 2^{x}, \quad$ c) $y=(-3) \cdot 2^{x}, \quad$ d) $y=0.2 \cdot 2^{x}, \quad$ e) $y=(-0.2) \cdot 2^{x}$
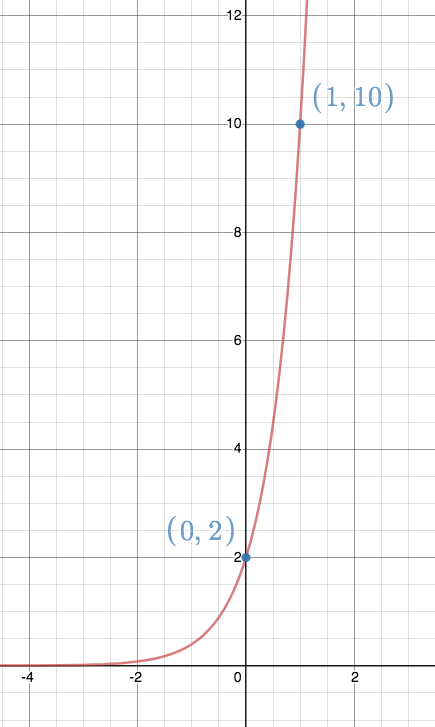
Example 3: The graph below shows an exponential function $f(x)$. Find a formula for $f(x)$.
Logarithmic Functions and their Graphs
Definition. If $b$ is a positive real number and $b\neq 1$, then the logarithm with base $b$ is defined:
$y=\log_b(x) \iff b^y=x$
What does the definition of logarithm mean? The idea is that the logarithm is the inverse function of the exponential function. Let’s look at an example.
Question: Is an exponential function one-to-one? (What does one-to-one means).
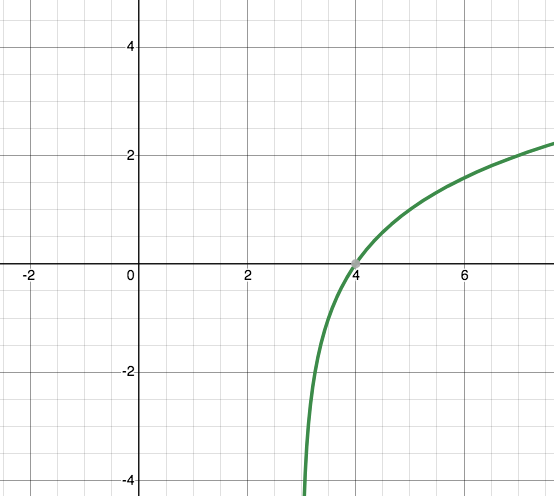
Example 4. The graph below shows the function $y=\log_2(x)$ but shifted to the right 3 units. Find a formula for the function in the graph.
That’s it for now! Take a look at the WeBWorK assignment, leave your questions below (or use the Ask for Help button in WeBWorK, or send me an email)
Print this page


0 Comments
6 Pingbacks