y= -0.2x^2
MAT1275 College Algebra w/ Trig, SP2017
View of Manhattan Bridge from Brooklyn Waterfront: an important object of our study will be the parabola
y= -0.2x^2
The OpenLab is an open-source, digital platform designed to support teaching and learning at City Tech (New York City College of Technology), and to promote student and faculty engagement in the intellectual and social life of the college community.
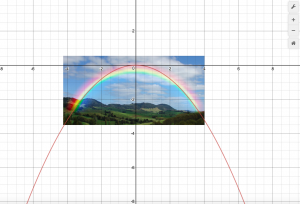
This submission is pretty close to what I was expecting as far as using desmos to get a graph which approximates the curve photographed. Good job! The origin has been placed at the vertex and since the parabola is upside down, the equation will be y=-a*x^2 where a is some positive number. However, with an enlarged picture, it would be more evident that a rainbow is in fact an arc (part of a circle). [You can see the entire circle in halos, which have similar optics to rainbows.] For further study, after enlarging the picture (or zooming in), superimpose the equation of a circle simultaneously with that of parabola. Use y=sqrt(r^2-x^2)-r, where r is the radius. The top of the circle would coincide with the origin. I am guessing that this would show that the circle is a better fit. When doing this, just use one color, say yellow. [In your superimposition, notice that your curve starts at one end of the spectrum (red) and goes to the other (violet).]