[Ezra Halleck]

1. The probability that an unfair coin lands on heads is 0.6. Coin is tossed 3 times.
a. List the sample space.
b. Construct a random variable X which counts number of heads for the three tosses.
c. Find P(X<1), E(X) and E(1/(X+1))

[Anonymous]

Is this the sample space? {HHH, THH, HTH, HHT, THT, TTH, HTT, TTT}.

[mendozak]

a.

S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

P (HHH) = .216
P (HHT) = P (HTH) = P (THH) = .144
P (HTT) = P (THT) = P (TTH) = .096
P (TTT) = .064

.216 + (3).144 + (3).096 + .064 = 1

b.

P (X = 3) = .216
P (X = 2) = .432
P (X = 1) = .288
P (X = 0) = .064

.216 + .432 + .288 + .064 = 1

c.

P (X<1) = P (X=0) = .064
E (X) = (3*(.216)) + (2*(.432)) + (1*(.288)) + (0*(.064)) = 1.8

[Ezra Halleck]

Good work! From the distribution, we can see a shifting of the middle towards the right (and skewing to the left). With a fair coin, the mean would be 1.5 rather than 1.8.

[Rob]

Visual representation of the problem as a tree

[Ziyuan Wu]

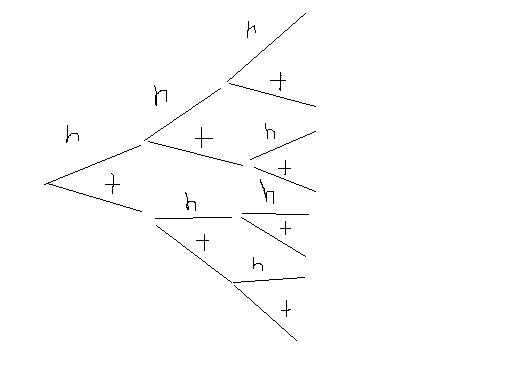
For the second part of (c), E(1/(X+1))

E(1/(X+1))=0.064+(0.288/2)+(0.432/3)+(0.216/4)=0.406

[Rob]

sorry for the rough sketch quality

[Nikoy O’Gilvie]

well looking at these solution from other persons are really helping to figure out where i went wrong. NICE WORK mendozak