In this lab you need to learn how to create a function called fruitful function, and how to define a language, finding definition on this language just like a translator also learn how to create a language in there or program it just like those programmer, will help you understand more of those language. So I think this lab was very helpful, maybe can help me learn more new language around the world too. This is the step you need to follow when you need to create a Fruitful Function:
In number theory, Fermat’s Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two. The cases n = 1 and n = 2 were known to have infinitely many solutions.
First problem.
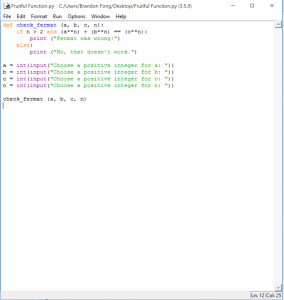
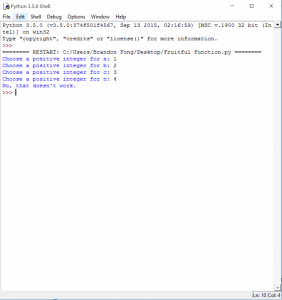
1. Write a function named check_fermat that takes four parameters—a, b, c and n and that checks to see if Fermat’s theorem holds. If n is greater than 2 and it turns out to be true that an + bn = cn the program should print, “Fermat was wrong!” Otherwise the program should print, “No, that doesn’t work.”
2. Write a function that prompts the user to input values for a, b, c and n, converts them to integers, and uses check_fermat to check whether they violate Fermat’s theorem.
Second problem.
In addition to the first problem, your code should let user make input and therefore to produce result.
Hint: use the built-in function <<raw_input>> and make the user input always be an integer.