What does it mean for two line segments OR triangles OR other subsets of the plane to be “the same shape”?
The concept of “shape”, the concept of “similarity”
What does it mean for two figures to be the “same shape but not the same size”? What does “shape” mean? We intuitively know the answer — how do we make it precise, mathematically?
The mathematical term we use for “same shape” is similarity. In TSM, there is a two-pronged approach to defining similarity.
- The very intuitive, very general approach: Two figures are similar if they have the same shape but not the same size.
- The very precise approach that applies only to triangles: Two triangles are similar if corresponding angles are equal and corresponding sides are proportional.
In order to talk more precisely about similarity, we need a tool to compare two different shapes of different sizes. This tool is a new transformation of the plane, much like the basic isometries (rotation, reflection, translation) we discussed last time, except that this one will NOT preserve distances (is NOT an isometry) — it will “change the size” of objects in the plane.
Basic facts about dilations
THEOREM. Let $D$ be a dilation with center $O$ and scale factor $r$. Then:
(a) For any segment $A B,|D(A B)|=r|A B|$.
(b) $D$ maps angles to angles and preserves degrees of angles.
How can we use the idea of Dilation to define when two subsets of the plane are “the same shape” (similar)? (Recall how defined congruence/congruent based on isometries).
Example. Are the two figures the same shape? Is one a dilation of the other?
Similarity
Definition. A similarity is a transformation of the plane that is the composition of a finite number of dilations and congruences.
Similar
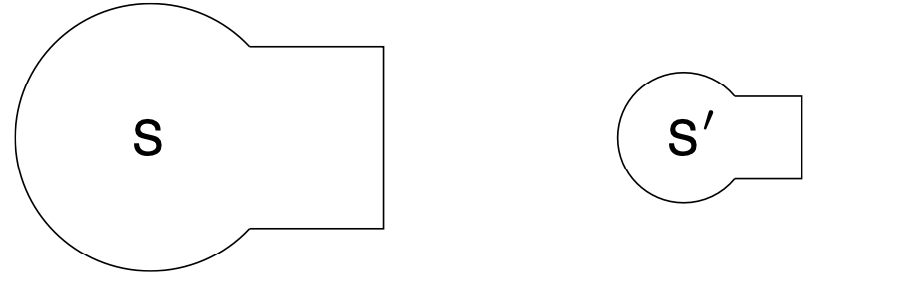
A subset $S$ of the plane is similar to another subset $S^\prime$ of the plane if there is a similarity $F$ so that $F(S)=S^\prime$. In symbols, we say $S \sim S^\prime$.
In the case of triangles, the notation we use for similarity carries additional information – in particular, it tells us which points in the first triangle correspond with which points in the second triangle.
We say $\triangle ABC \sim \triangle A^\prime B^\prime C^\prime $ if there is a similarity $F$ so that $F(A)=A^\prime$, $F(B)=B^\prime$, $F(C)=C^\prime$.
What does it mean for triangles to be similar?
Similar Triangles
THEOREM G 20. Given two triangles $A B C$ and $A^{\prime} B^{\prime} C^{\prime}$, then $\triangle A B C \sim \triangle A^{\prime} B^{\prime} C^{\prime}$, if and only if
$$
|\angle A|=\left|\angle A^{\prime}\right|, \quad|\angle B|=\left|\angle B^{\prime}\right|, \quad|\angle C|=\left|\angle C^{\prime}\right|
$$
and
$$
\frac{|A B|}{\left|A^{\prime} B^{\prime}\right|}=\frac{|A C|}{\left|A^{\prime} C^{\prime}\right|}=\frac{|B C|}{\left|B^{\prime} C^{\prime}\right|}
$$
Note: The first part says “corresponding angles are equal”, the second part says “corresponding sides are proportional.”
AA theorem
Theorem G22 (AA for similarity). Two triangles with two pair of equal angles are similar.





Leave a Reply