The main issues [with TSMs treatment of geometry] may be summarized as follows:
- The high school geometry course cannot be the only place in the K–12 curriculum where definitions, theorems, and proofs are taken seriously. To the extent that we are trying to teach students mathematics with mathematical integrity rather than some latter-day concoction that purports to be “mathematics”, we have to make the rest of the school mathematics curriculum take definitions, theorems, and proofs seriously too. The use of an axiomatic system in the high school geometry course is a more complex issue and will have to be handled with some care.
- Congruence and similarity are not only the bedrock of the high school geometry course and a foundation of high school algebra, they are also a mainstay of the whole school geometry curriculum. We must find definitions for these two concepts so that they are usable in both middle school and high school.
- The curricular decision by TSM to make students work with slope in introductory algebra before teaching them about similar triangles has caused great harm in students’ learning of slope (see [PG], for example). We have to provide students with the necessary mathematical knowledge about similar triangles before the introduction of slope. This will improve students’ ability to learn about slope and strengthen the relevance of the high school geometry course to the school mathematics curriculum.
– Wu, RLE
The concept of distance or length
Our geometric intuition is grounded in our experience of the real world. For many basic concepts in geometry, that intuition is a great (indeed, fantastic) tool! However, it can be helpful to recognize some of the underlying assumptions we make about geometry and geometric objects that come from our real-world experience.
What does it mean for two line segments OR triangles OR other subsets of the plane to be “the same”?
Many basic concepts will not be defined here — for example, point, line, plane, angle, and so on (you can take a look at Wu RLE Chapters 4 and 5 for a detailed exposition of basic concepts). It’s also important to note at the outset that the geometry curriculum does NOT make use of a coordinate plane (complete with x- and y- axes, etc), but just a “plain plane” – so things like coordinates of points, and the use of equations to describe lines and other figures, will not appear.
The concept of the length of a segment in the plane is far from simple; it can only be fully understood in the context of rotations, translations, and reflections of the plane.
Wu, RLE
The basic notion that will describe so much of our work in the plane is called a transformation – a function from the plane to itself.
Transformation
Let $\Pi$ denote the plane. A transformation $F$ of $\Pi$ is a rule that assigns to each point $P$ of $\Pi$ a unique point $F(P)$ (read: “$F$ of $P$” ) in $\Pi$.
We also say $F$ maps $P$ to $F(P)$ or, sometimes, $F$ moves $P$ to $F(P)$. Indeed, it is intuitively appealing to think of a transformation as a way of “moving” the points of the plane around.
Two examples of transformations, very different in character:
I. The identity transformation I which maps every point $P$ to itself (the “do nothing” transformation).
II. For a point $X$, the constant transformation $F_X$ which sends every point in the plane to $X$.
Isometry
A transformation $F$ is an isometry if it preserves distances/lengths. That is, if $\operatorname{dist}(P,Q) = \operatorname{dist}(F(P),F(Q))$ for all $P, Q$ in $\Pi$.
Is the identity transformation an isometry? How about a constant transformation?
NOTE: Preserving distance is a very strong property – in fact, any isometry also preserves angles, maps lines to lines and circles to circles, and so on.
The basic isometries
Rotation around a point $P$ by angle $t$ ($t$ is measured in degrees, if $t$ is positive then the rotation is counterclockwise, if $t$ is negative the rotation is clockwise).
Reflection across a line $L$.
Translation along a vector $\overrightarrow{AB}$.
Note that we can do multiple transformations in a row, and the result is a new transformation – this exactly corresponds to composition of functions.
Question: If we do multiple isometries in a row, is the result an isometry?
Example
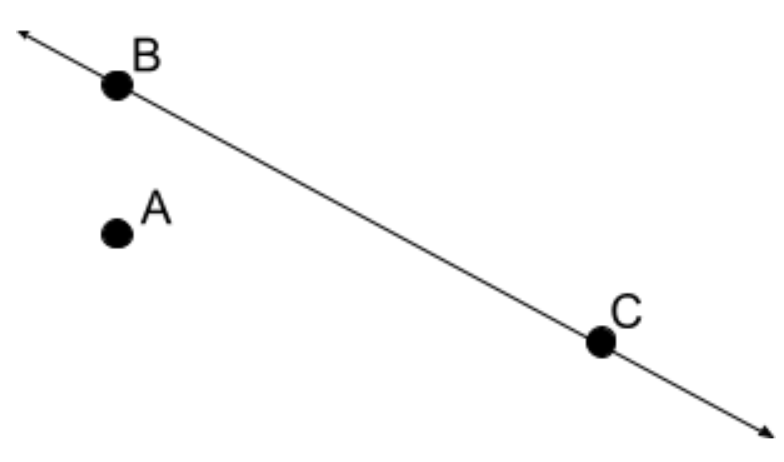
Suppose $F$ is the rotation of $90^\circ$ about the point $A$, and $G$ is the reflection across the line $\overline{BC}$.
- Locate $F(B), F(C), F(A)$ (referred to as the image of B, C, and A under the transformation $F$).
- Locate $G(A), G(B), G(C)$.
Now suppose we *first* do $F$, followed by $G$.
- Locate $G(F(B)), G(F(C)), G(F(A))$.
- Locate $F(G(B)), F(B(C)), F(G(A))$.
Congruence
Definition. A congruence is a transformation of the plane that is the composition of a finite number of basic isometries.
Congruent
A subset $S$ of the plane is congruent to another subset $S^\prime$ of the plane if there is a congruence $F$ so that $F(S)=S^\prime$. In symbols, we say $S\cong S^\prime$.



0 Comments
2 Pingbacks