Hi everyone,
I wanted to give an example of writing a given set in set-theoretic notation – this should help out with some of the problems on your first homework assignment (Section 1.1).
Example: Write in set-theoretic notation:
In this case, you can see that the given set consists of all multiples of 5. A good way to approach problems like this is to start with one of the basic sets, for example
- the natural numbers
- the integers
In this example, I can see that multiplying every natural number by 5 should give me the set that I want. Therefore, I will use the formula 
Solution
Here are two ways to read this solution aloud:
- “the set of all
such that
is a natural number”, or
- “for each
and include the result in the set”
I hope this helps – feel free to respond here if you any questions.
Best,
Prof. Reitz
Dear Prof. Reitz,
Thank you for the examples. It helped me for the homework. But, I have confused about the question: {x is an element of “Z” : |2x| <5}. Can you please explain me little bit about this question?
Sincerely,
Fuzail
Hi Fuzail,
This one looks a little strange, because we are expecting a formula to come first, and instead we have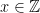
. This is something common in mathematics that doesn’t exactly follow the rule, in which we describe the type of number (integers) in the first part of the set-theoretic notation – really, it means the same thing as this: 
.
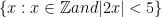I hope this helps – feel free to write back if not.
-Prof. Reitz